
Question and Answers Forum
IntegrationQuestion and Answers: Page 123


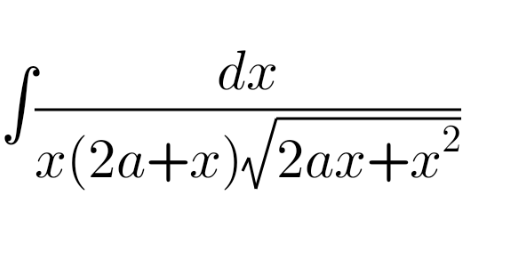

Pg 118 Pg 119 Pg 120 Pg 121 Pg 122 Pg 123 Pg 124 Pg 125 Pg 126 Pg 127
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 123 |
| Find the polynomial P(x) of least degree that has a maximum equal to 6 at x=1 and minimum equal to 2 at x=3. |
| ...advanced calculus... prove that : Re(∫_0 ^( (π/2)) sin^3 (x)ln(ln(cos(x)))dx) =^? ((ln(3)−2γ)/3) ✓ |
| calculate A_n =∫_0 ^∞ (dx/((x^2 +1)(x^2 +2)....(x^2 +n))) wth n integr natural and n≥1 |
| ...nice calculus... prove that : Σ_(n=1 ) ^∞ {((ζ(2n+1)−1)/(n+1))}=−γ+ln(2)✓ ..m.n.1970.. |
| ... nice calculus... calculate :: Ω=∫_0 ^( 1) x^2 (ψ(1+x)−ψ(2−x))dx=??? .m.n.1970. |
| ∫ ((√(1−(√x)))/( (√(1+(√x))))) dx ? |
| find ∫ (dx/(x(x+1)(√(x^2 +x)))) |
| Obtain a reduction formulae for I_n = ∫_0 ^1 (ln x)^n dx find I_2 = ∫_0 ^1 (ln x)^2 dx |

|
| ... nice calculus... prove that:: Ω=∫_0 ^( (π/2)) {tan^(−1) (ptan(x))−tan^(−1) (qtan(x))}(tan(x)+cot(x))dx =(π/2) log((p/q)) ( p , q >0 ) m.n. |
| find ∫_(−1) ^1 (√(1+x^4 ))dx |
|
| ∫_0 ^3 (1/( (√y))).e^y dy |

|
| ∫_1 ^2 ((ln (x))/x^2 ) dx ? |
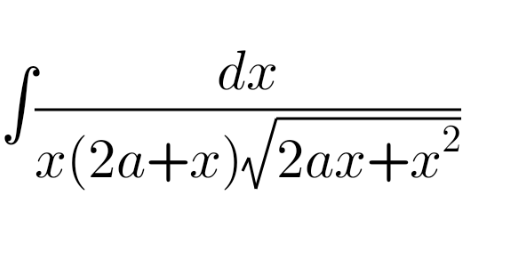
|
|
| ...nice calculus... prove that : ∫_0 ^( 1) ((ln^2 (1+x))/x)dx=^(??) ((ζ(3))/4) .m.n. |
| ∫_0 ^( ∞) e^(−x^2 ) cos(5x)dx |
| ∫_4 ^9 ((ℓn (x))/( (√x))) dx ? |
| ∫_0 ^1 (dx/( ((x^2 −x^3 ))^(1/(3 )) )) ? |
| Σ_(n=0) ^∞ ((1/(12n+1))+(1/(12n+5))−(1/(12n+7))−(1/(12n+11))) Problem source : Brilliant.Org |
|

|
|
| 1)explicite f(a)=∫_0 ^∞ ((t^(a−1) lnt)/(1+t))dt with 0<a<1 2)calculate ∫_0 ^∞ ((lnt)/((1+t)(√t)))dt |
Pg 118 Pg 119 Pg 120 Pg 121 Pg 122 Pg 123 Pg 124 Pg 125 Pg 126 Pg 127 |