
Question and Answers Forum
IntegrationQuestion and Answers: Page 126


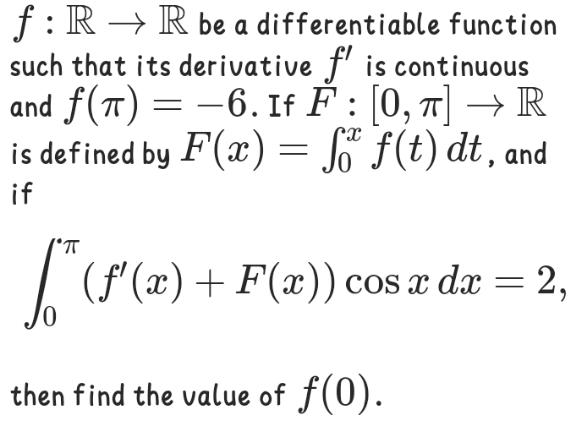
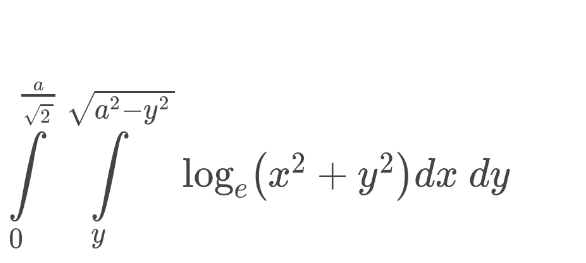
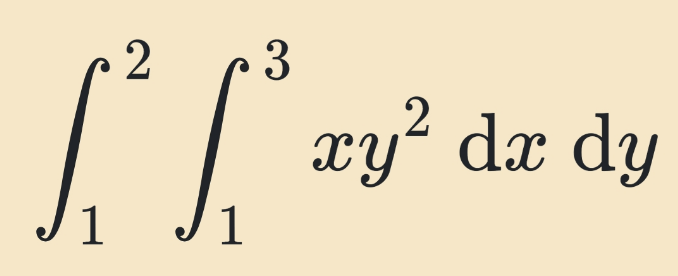
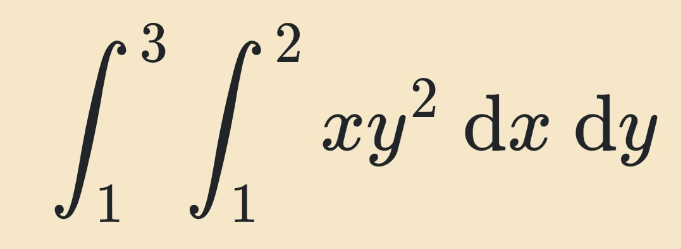

Pg 121 Pg 122 Pg 123 Pg 124 Pg 125 Pg 126 Pg 127 Pg 128 Pg 129 Pg 130
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 126 |
| find ∫ (dx/((x−1)(√(x+1))−(x+1)(√(x−1)))) |
| decompose F(x) =(x^n /(x^(2n+1) +1)) 2)find the value of ∫_0 ^∞ (x^n /(x^(2n+1) +1))dx n integr natural |
| find ∫_0 ^∞ xe^(−x^2 ) arctan(2x)dx |

|

|
| ∫ (dx/(x−4(√x))) ? |
|
| ... advanced calculus... evaluate: Σ_(n=1) ^∞ (((H_n )^2 )/n^2 ) =? where H_n =Σ_(k=1) ^n (1/k) (harmonic number) |
| The tangent line to y = f(x) at (3,4) is given y=3x−5. What is the tangent line to y = f^(−1) (x) at (3,4) where f(x) is an injective continous function that satisfies f(3)=4. |
|
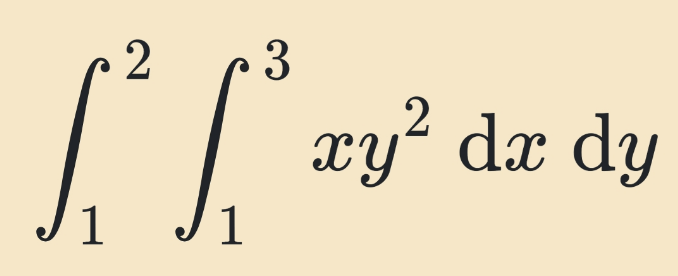
|
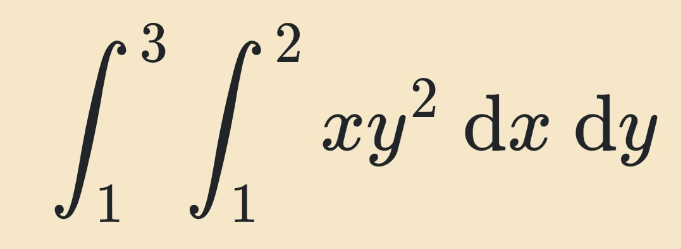
|
| ∫ ((x^4 −5x^3 +6x^2 −18)/(x^3 −3x^2 )) dx ? |
| please evaluate ∫x^x dx |
| ... advanced calculus... prove that : Ω =∫_0 ^( ∞) ((sin^4 (x)ln(x))/x^2 )dx=(π/4)(1−γ) γ:euler−mascheroni constant m.n.july.1970 |
| ∫_0 ^2 sin (2πx)cos (5πx) dx ? |

|
| ∫ (dx/(x (√(3+x^2 )))) ? |
| ∫_0 ^(π/4) tan^6 x sec x dx =? |
| ∫ ((1−x^4 )/(x^2 (√(x^4 +x^2 +1)))) dx ? |
| Evaluate Σ_(n=1) ^∞ ((sin(n))/n) |
| (1) ∫ (dx/(x^4 +2x^2 +9)) ? (2) arc tan ((x/3))−arc tan ((x/3))= arc tan ((1/5)) |
| calculate ∫_0 ^(+∞) (dx/((x^4 +1)^3 )) |
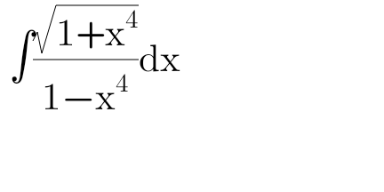
|
| ∫(√(cos(x) dx)) |
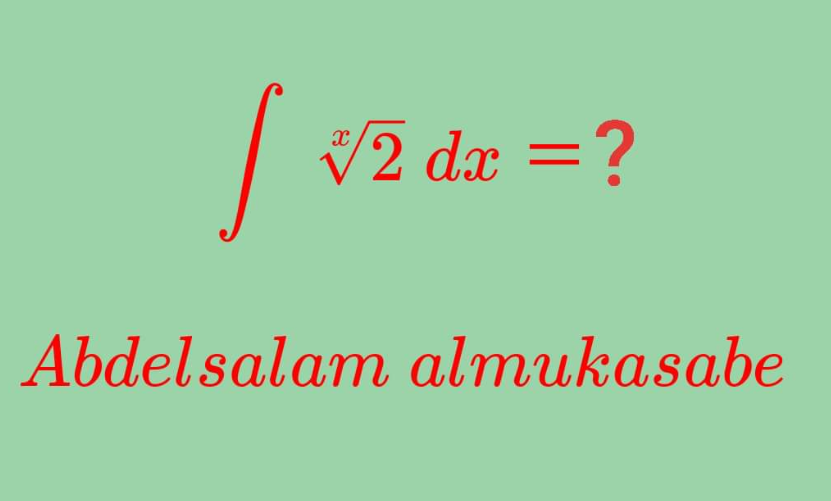
|
Pg 121 Pg 122 Pg 123 Pg 124 Pg 125 Pg 126 Pg 127 Pg 128 Pg 129 Pg 130 |