
Question and Answers Forum
IntegrationQuestion and Answers: Page 127





Pg 122 Pg 123 Pg 124 Pg 125 Pg 126 Pg 127 Pg 128 Pg 129 Pg 130 Pg 131
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 127 |
| evaluate: ∫_0 ^( ∞) ((x/(x+1)) − lim_(k→∞) ((k/(k+1)))^(⌊k⌋) )^(⌊x⌋) dx |

|
| ... Nice calculus... evaluate :: S= Σ_(n=1) ^∞ ((2^(−2n) /(1+cos((π/2^n )))))=?? ...M.N.1970... |
| ...advanced calculus... evaluate :: Φ=^(???) ∫_0 ^( 1) ln(x)tan^(−1) (x)dx ...m.n.1970... |
| ...advanced calculus... prove that :: Ω=∫_0 ^( 1) ((ln(x))/( ((1−x^3 ))^(1/3) ))dx=^(???) −(π/(3(√3)))(ln(3)+(π/(3(√3)))) ...m.n.1970... |
| ∫ tan^(−1) ((√((1−x)/(1+x))) ) dx ? |
| ∫ (dx/(a sin x + b cos x)) |
| ∫ (dx/(x^2 (√(9+x^2 )))) ? |
| ∫_0 ^π ((x dx)/(1+sin^2 x)) |
| selective intregals |
| Let x = u^6 dx = 6u^5 du I = ∫(u^3 /((1+u^2 )^2 )) ×6u^5 du =6 ∫(u^8 /(1+2u^2 +u^4 )) du =6 ∫[((−4)/(u^2 +1))+(1/((1+u^2 )^2 ))+u^4 −2u^2 +3]du =6[−4tan^(−1) (u) + I_1 + (u^5 /5) − (2/3)u^3 +3u]+c I_1 = ∫(1/((1+u^2 )^2 )) du Put u = tan z du = sec^2 z dz I_1 = ∫(1/(sec^4 z))×sec^2 z dz = ∫cos^2 z dz = ∫(1/2)(cos 2z + 1)dz = (1/2)((1/2) sin 2z + z) = (1/2)×(u/(1+u^2 )) + (1/2) tan^(−1) u I = −4 tan^(−1) u + (u/(2(1+u^2 ))) + (1/2) tan^(−1) u +(u^5 /5) − (2/3)u^3 + 3u + c = −(7/2) tan^(−1) u + (u/(2(1+u^2 ))) + (1/5)u^5 + 3u + c = −(7/2) tan^(−1) ( ^6 (√x)) + ((x)^(1/6) /(2(1+(x^2 )^(1/6) ))) + (1/5) (x^5 )^(1/6) + 3 (x)^(1/6) + c |
| Let u=x^(3/5) du = (3/(5x^(2/5) )) I = (5/3)∫(u/( (√(3−2u)))) du = −(5/6) ∫((3−2u−3)/( (√(3−2u)))) du = −(5/3) ∫[(√(3−2u)) −3(3−2u)^(−(1/2)) ] du = −(5/3)[−(1/3)(3−2u)^(3/2) +3(3−2u)^(1/2) ]+c = −(5/(18))(3−2u)^(1/2) [−3+2u + 9]+c = −(5/(18))(3−2u)^(1/2) (6+2u)+c = −(5/9)(√(3−2x^(3/5) ))(3+x^(3/5) )+c |

|
| Prove that for all a>0 ∫_([−a;a]) arg(Γ((1/2) −ix))dx =0 Deduce that f: x→arg(Γ((1/2) −ix)) is an old function on R |
| evaluate: ∫_0 ^( ∞) ((x/(x+1)))^(x!) dx |

|
| ∫(1/((cos x)^6 ))=? |
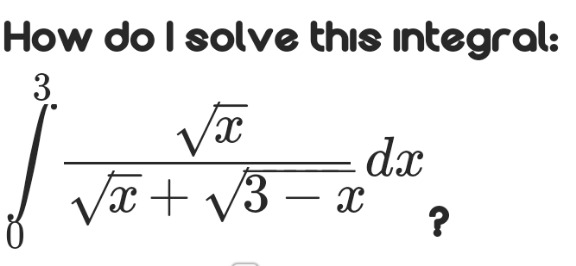
|

|
| ∫ ((√(1+x^2 ))/x) dx |

|
| calculate ∫_0 ^(π/2) ((xcosx)/(cos(2x)))dx |
| ∫_0 ^(π/2) ((x dx)/(sin x+cos x)) |
| calculate ∫_2 ^∞ (dx/((x^2 −1)^2 (x^2 +x+1))) |
| fond ∫_2 ^∞ ((ln(1+3x^2 ))/(1+x^4 ))dx |
| ∫ ((f ′(x))/(f(x))) =? |
Pg 122 Pg 123 Pg 124 Pg 125 Pg 126 Pg 127 Pg 128 Pg 129 Pg 130 Pg 131 |