Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 128

Question Number 118752 Answers: 0 Comments: 0

∫ ((2 dx)/(x^2 (((3+x^4 )^5 ))^(1/(4 )) )) dx

$\int \frac{2 d x}{x^{2} \sqrt[4]{{(3 + x^{4})}^{5}}} d x$

Question Number 118710 Answers: 2 Comments: 0

Question Number 118705 Answers: 2 Comments: 0

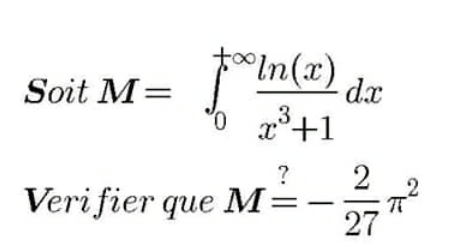
... ⧫Advanced Calculus⧫... Evaluate:: Ω = ∫_0 ^( 1 ) ((sin^(−1) (x))/(1+x^2 ))dx ...♠L𝛗rD ∅sE♠... ...♣GooD LucK♣

$. . . ⧫ Advanced Calculus ⧫ . . .$ $Evaluate ::$ $Ω = \int_{0}^{1} \frac{\sin^{- 1} (x)}{1 + x^{2}} dx$ $. . . ♠ L ϕ rD \emptyset sE ♠ . . .$ $. . . ♣ GooD LucK ♣$

Question Number 118668 Answers: 1 Comments: 0

∫ ((x∣sin x∣)/(1+cos^2 x)) dx ?

$\int \frac{x ∣ \sin x ∣}{1 + \cos^{2} x} d x ?$

Question Number 118679 Answers: 2 Comments: 0

Question Number 118663 Answers: 1 Comments: 2

Given f(x) = ∫ _0 ^x (dt/([f(t)]^2 )) and ∫ _0 ^2 (dt/([ f(t)]^2 )) = (6)^(1/(3 )) Then then the value of f(9) is __

$G i v e n f (x) = \int \underset{0}{\overset{x}{}} \frac{d t}{{[f (t)]}^{2}} a n d \int \underset{0}{\overset{2}{}} \frac{d t}{{[f (t)]}^{2}} = \sqrt[3]{6}$ $T h e n t h e n t h e v a l u e o f f (9) i s__$

Question Number 118575 Answers: 1 Comments: 0

∫ cos (2cot^(−1) (√((1−x)/(1+x))) ) dx ?

$\int \cos ({2 \cot}^{- 1} \sqrt{\frac{1 - x}{1 + x}}) d x ?$

Question Number 118566 Answers: 6 Comments: 2

solve ∫_0 ^1 (dx/( (√x) (√(1−x)) )) .

$s o l v e \underset{0}{\int^{1}} \frac{d x}{\sqrt{x} \sqrt{1 - x}} .$

Question Number 118541 Answers: 3 Comments: 1

∫ tan (x).tan (2x).tan (3x) dx = ?

$\int \tan (x) . \tan (2 x) . \tan (3 x) d x = ?$

Question Number 121164 Answers: 0 Comments: 0

...ADVANCED CALCULUS... If ∫_0 ^( ∞) ln(x)sin(x^2 )dx =λ∫_0 ^( ∞) sin(x^2 )dx then find the value of ′′λ′′ . ...m.n.july.1970...

$. . . ADVANCED CALCULUS . . .$ $If \int_{0}^{\infty} l n (x) s i n (x^{2}) d x = λ \int_{0}^{\infty} s i n (x^{2}) d x$ $t h e n f i n d t h e v a l u e o f^{″} λ^{″} .$ $. . . m . n . july . 1970 . . .$

Question Number 118491 Answers: 1 Comments: 0

... ⧫Advanced Calculus⧫... Evaluate:: Ω = ∫_0 ^( ∞) ((secθ)/( (√(4tan^2 θ+5))))dθ ...♠L𝛗rD ∅sE♠... ...♣GooD LucK♣

$. . . ⧫ Advanced Calculus ⧫ . . .$ $Evaluate ::$ $Ω = \int_{0}^{\infty} \frac{\sec θ}{\sqrt{{4 \tan}^{2} θ + 5}} d θ$ $. . . ♠ L ϕ rD \emptyset sE ♠ . . .$ $. . . ♣ GooD LucK ♣$

Question Number 118478 Answers: 0 Comments: 0

find ∫_0 ^∞ e^(−2x) ln(1+3x)dx

$find \int_{0}^{\infty} e^{- 2 x} \ln (1 + 3 x) dx$

Question Number 118476 Answers: 0 Comments: 0

find ∫_(−∞) ^∞ ((arctan(1+2x))/(x^2 +1))dx

$find \int_{- \infty}^{\infty} \frac{\arctan (1 + 2 x)}{x^{2} + 1} dx$

Question Number 118475 Answers: 0 Comments: 0

calculate ∫_0 ^∞ ((arctan(2+x^2 ))/(x^2 +9))dx

$calculate \int_{0}^{\infty} \frac{\arctan (2 + x^{2})}{x^{2} + 9} dx$

Question Number 118438 Answers: 0 Comments: 0

... nice calculus... evaluate :: lim_(s→0) ((ζ( 1+s )+ζ(1−s))/2) =^? γ γ: euler−mascheroni constant m.n.1970.

$. . . n i c e c a l c u l u s . . .$ $e v a l u a t e ::$ ${l i m}_{s \to 0} \frac{ζ (1 + s) + ζ (1 - s)}{2} \overset{?}{=} γ$ $γ : e u l e r - m a s c h e r o n i c o n s t a n t$ $m . n . 1970 .$

Question Number 118436 Answers: 4 Comments: 0

∫ cos^4 (x) cos^4 (2x) dx

$\int \cos^{4} (x) \cos^{4} (2 x) d x$

Question Number 118419 Answers: 4 Comments: 1

∫ ((2sin 2x)/(4cos x+sin 2x)) dx

$\int \frac{2 \sin 2 x}{4 \cos x + \sin 2 x} d x$

Question Number 118395 Answers: 2 Comments: 5

∫_a ^b ((f(x))/(f(x)+f(a+b−x)))dx

$\int_{a}^{b} \frac{f (x)}{f (x) + f (a + b - x)} d x$

Question Number 207620 Answers: 1 Comments: 0

prove that ∫_(−a) ^a (dx/(x^n +1+(√(x^(2n) +1))))=a

$prove that \underset{- a}{\int^{a}} \frac{d x}{x^{n} + 1 + \sqrt{x^{2 n} + 1}} = a$

Question Number 118347 Answers: 1 Comments: 0

∫ (dx/( (√x) +(x)^(1/(3 )) ))

$\int \frac{d x}{\sqrt{x} + \sqrt[3]{x}}$

Question Number 118340 Answers: 1 Comments: 1

∫_(π/3) ^(π/2) (dx/(1+sin x−cos x))

$\underset{π / 3}{\int^{π / 2}} \frac{d x}{1 + \sin x - \cos x}$

Question Number 118338 Answers: 3 Comments: 0

solve ∫ (dx/(3−5sin x))

$s o l v e \int \frac{d x}{3 - 5 \sin x}$

Question Number 118318 Answers: 1 Comments: 0

Question Number 118307 Answers: 2 Comments: 1

∫^∞ _0 ((x^2 −2)/(x^4 +x^2 +1)) dx

${\int_{0}}^{\infty} \frac{x^{2} - 2}{x^{4} + x^{2} + 1} d x$

Question Number 118292 Answers: 2 Comments: 0

Prove that: ∫_0 ^( 1) ((x^n −1)/(lnx)) = ln∣n+1∣

$P rove that :$ $\int_{0}^{1} \frac{x^{n} - 1}{lnx} = \ln ∣ n + 1 ∣$

Question Number 118270 Answers: 0 Comments: 1

∫x a^x (1−a)^(1−x) dx?

$\int x a^{x} {(1 - a)}^{1 - x} d x ?$

Pg 123 Pg 124 Pg 125 Pg 126 Pg 127 Pg 128 Pg 129 Pg 130 Pg 131 Pg 132

Contact: info@tinkutara.com