
Question and Answers Forum
IntegrationQuestion and Answers: Page 129

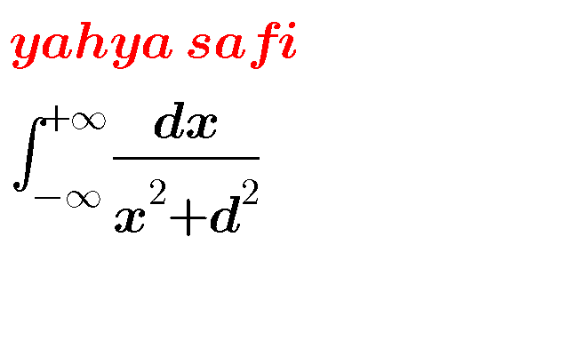

Pg 124 Pg 125 Pg 126 Pg 127 Pg 128 Pg 129 Pg 130 Pg 131 Pg 132 Pg 133
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 129 |
| lim_(n→∞) n^2 ∫ _0 ^(1/n) x^(x+1) dx =? |
| ∫ (dx/( (√((4x−x^2 )^3 )))) |
| ∫_(−4) ^4 x^3 (√(16−x^2 )) sec x dx |
| ∫_(−3) ^0 ((6x−6)/( (√(x^2 −2x+1)))) dx =? |
| calculate ∫_0 ^∞ ((x^4 dx)/((2x+1)^5 (3x+1)^8 )) |
| find I_λ =∫_0 ^∞ ((ch(1+λcosx))/((x^2 +1)^2 ))dx (λ real >0) |
| Π_(k=1) ^(1019) [((2k)/(2k−1))]=? |
| For a<b then ∫_a ^b (x−a)(x−b) dx equal to _ |
| ∫_0 ^π (√((1+cos2x)/2)) dx ∫_0 ^∞ [ne^(−x) ]dx |
| ... ♣_♣ ^♣ nice calculus♣_♣ ^♣ ... prove that :: Ω=∫_0 ^( ∞) e^(−2x) ln(((1+e^(−x) )/(1−e^(−x) )))=1 ...★ M.N.1970★... |
| ...nice calculus... prove that :: ∫_0 ^( (π/2)) (√(((2^x −1)sin^3 (x))/((2^x +1)(sin^3 (x)+cos^3 (x))))) dx<(π/8) ...m.n.1970... |
| ... advanced calculus... evaluate :: Ω=∫_0 ^( ∞) ((tan^(−1) (x))/(e^(2πx) −1))dx =? m.n.1970 |
| calculste ∫_0 ^∞ ((ln(2+x^2 ))/(1+x^3 ))dx |
| ...nice calculus... prove that:: Σ_(n=1) ^∞ (((−1)^(n−1) )/(n^3 (((2n)),(n) ))) =^(???) ζ(3) m.n.1970 |
| ... advanced calculus... prove that : Σ_(n=1) ^∞ (1/(n^2 (((2n)),(n) ))) =^(???) ((ζ(2))/3) solution:: Σ_(n=1) ^∞ (1/(n^2 ∗(((2n)!)/((n!)^2 ))))=Σ_(n=1) ^∞ ((n!∗n!)/(n^2 ∗(2n)!)) =Σ_(n=1) ^∞ ((Γ(n)Γ(n+1))/(nΓ(2n+1)))=Σ_(n=1) ^∞ ((β(n,n+1))/n) =Σ_(n=1) ^∞ (1/n)∫_0 ^( 1) x^(n−1) (1−x)^n =∫_0 ^( 1) (1/x)Σ(((x−x^2 )^n )/n)dx =−∫_0 ^( 1) ((ln(1−x+x^2 ))/x)dx =−∫_0 ^( 1) ((ln(1+x^3 )−ln(1+x))/x)dx =∫_0 ^( 1) ((ln(1+x))/x)dx −∫_0 ^( 1) ((ln(1+x^3 ))/x)dx =−li_2 (−1) −∫_0 ^( 1) ((Σ_(n=1) (((−1)^(n+1) x^(3n) )/n))/x) dx =(π^2 /(12))+Σ_(n=1) ^∞ (((−1)^n )/n)∫_0 ^( 1) x^(3n−1) dx =(π^2 /(12)) +(1/3)Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =(π^2 /(12))−(π^2 /(36)) =(π^2 /(18)) =((ζ(2))/3) ✓✓ m.n.july.1970.. |
| decompose F(x) =((2x−1)/((x^2 −1)^2 (x^2 +3))) and calculate ∫_(√2) ^(+∞) F(x)dx |
| Express f(x) = (1/((x−1)^2 (x^2 +1))) into partial fractions. hence evaluate I = ∫_0 ^4 f(x) dx |

|
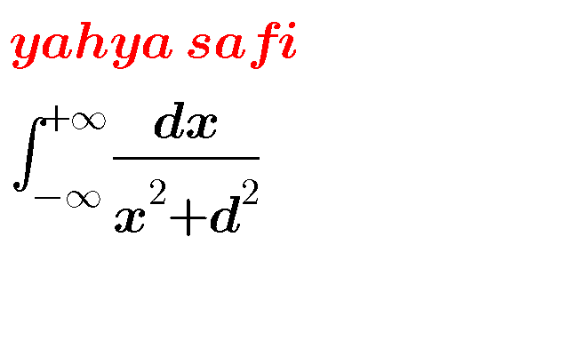
|
| ... nice calculus... evaluate:: I:= ∫_0 ^( 1) li_2 (1−x^2 )dx=?? .m.n.1970. |
| find ∫_0 ^∞ ((lnx)/(x^4 +x^2 +2))dx |
| calculate ∫_0 ^(2π) (dθ/((x^2 −2cosθ x+1)^2 )) |
| ∫ (x^2 /( (√((4−x^2 )^5 )))) dx |
| Determine ∫_(−(π/4)) ^( (π/4)) (cost+(√(1+t^2 sin^3 tcos^3 t))dt=? |

|
| ∫ ((x^2 −x+6)/(x^3 +3x)) dx ∫ ((5x^2 +3x−2)/(x^3 +2x^2 )) dx |
Pg 124 Pg 125 Pg 126 Pg 127 Pg 128 Pg 129 Pg 130 Pg 131 Pg 132 Pg 133 |