
Question and Answers Forum
IntegrationQuestion and Answers: Page 137

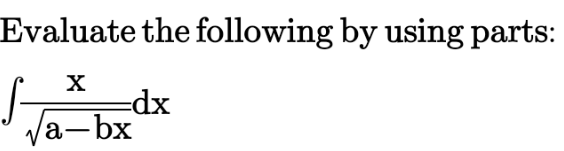
Pg 132 Pg 133 Pg 134 Pg 135 Pg 136 Pg 137 Pg 138 Pg 139 Pg 140 Pg 141
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 137 |
| ∫(1/(sinx + cosx))dx |
| calculate ∫_2 ^(+∞) (dt/((2t+3)^4 (t−1)^5 )) |
| ... advanced calculus... i : prove that :: ∫_0 ^( 1) ((ln(1+ln(1−x)))/(ln(1−x))) dx =^? Σ_(n=1) ^∞ ((Γ(n+1))/n^2 ) ii: prove that :: Ω =∫_0 ^( 1) ((ln(1+x))/(x(1+x^2 )))dx =^? ((5π^2 )/(48)) m.n.july 1970# |
| old and unanswered... Mr Mathdave??? ∫x^2 ln(1−x)ln(1+x)dx=? |
| ∫(x+1)^2 (1−x)^5 dx |
| (1)∫_0 ^π ((sin^4 x)/((1+cos x)^2 )) dx ? (2) lim_(x→∞) ((√(1−cos (((2π)/x))))/(1/x)) ? |
| ∫ (√x) cos ((√x)) dx |
| Find the area between the circle ρ=2acosθ and cardiode ρ=a(1+cosθ) |
| ∫_3 ^6 ((x+1)/(x^3 +x^2 −6x))dx |
| Consider the series I_n =∫_1 ^e x(lnx)^n dx and I_0 =∫_1 ^e xdx Which of the following is true ? a\ 0≤I_n ≤(e^2 /(n+2)) b\1≤I_n ≤(e^2 /(n+1)) c\I_n is negative |
| ∫_0 ^(π/2) ln(2−sinx)dx |
| I=∫_0 ^∞ ((π/(1+π^2 x^2 ))−(1/(1+x^2 )))lnx dx put πx=tanA, x =tanB I=∫_0 ^(π/2) (ln(tanA)−lnπ)dA−∫_0 ^(π/2) ln(tanB)dB I=((−π)/2)lnπ |
| ∫(√((x−1)/x^5 ))dx |

|
| ∫_0 ^π ((x sin x)/(1+cos^2 x)) dx ? |
| ∫ (dx/(tan x−sin x)) ? |
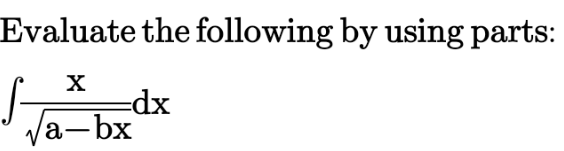
|
| ∫ (((1+tan (((3x)/2)))^2 )/(1+sin 3x)) dx ? |
| Bonjour besoin d′aide Calculer ∫ln(cosx)dx |
| explicit g(a) =∫_0 ^(π/4) ln(1+acos^2 θ)dθ |
| find f(a) =∫_0 ^(π/8) ln(1+a sinθ)dθ with o<a<1 |
| Prouver que β(a,b)=((Γ(a)Γ(b))/(Γ(a+b)))=∫_0 ^1 x^(a−1) (1−x)^(b−1) dx |
| find ∫ (dx/((x+1)(√(x^2 −1))+(x−1)(√(x^2 +1)))) |
| calculate ∫_0 ^∞ (dx/(x^4 +ix^2 +2)) |
|
| ∫_1 ^2 f(2x+1) dx = 3 and ∫_1 ^2 (x^2 f(x^3 +2))dx = 5 then ∫_5 ^(10) f(x) dx = ? |
Pg 132 Pg 133 Pg 134 Pg 135 Pg 136 Pg 137 Pg 138 Pg 139 Pg 140 Pg 141 |