
Question and Answers Forum
IntegrationQuestion and Answers: Page 141



Pg 136 Pg 137 Pg 138 Pg 139 Pg 140 Pg 141 Pg 142 Pg 143 Pg 144 Pg 145
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 141 |
| please evaluate : .... I=∫_0 ^( (π/2)) ((1/(ln(tan(x)))) + (1/(1−tan(x))))dx =??? ::: M. N.july 1970 ::: |
| ∫_0 ^1 ((tan^(−1) x)/(1+x^3 ))dx |
| (√(bemath)) ∫ (dx/( ((x−1))^(1/(3 )) (((x+1)^2 ))^(1/(3 )) )) ? |
| (1) ∫ (((x+1)dx)/(x^4 (x−1))) ? (2) (dy/dx) + (y/(x−2)) = 5(x−2)(√y) |
| following the newest trend − what do I say!? − ahead of it, of course! I post this answer to one of the next questions, look out for it so you won′t miss it! I=I_1 −2I_2 =ξ(5)+Γ(7/3)−2/(√π)+C |

|

|
|
| (√(bemath)) (1)∫ (dx/(3sin x+sin^3 x)) (2) lim_(x→∞) x(5^(1/x) −1) (3) find the asymptotes (x^2 /a^2 ) − (y^2 /b^2 ) = 1 |
| [∫_0 ^∞ JS dx ] ∫_0 ^(π/2) ((sin (x)(4+sin^2 (x)))/((4−sin^2 (x))^2 )) dx ? |
| ★((log _(JS) (farmer))/)★ (1)∫ ((tan (ln x)tan (ln ((x/2)))dx)/x) (2) sin (cos x) < cos (sin x) ; where 0≤x≤2π |
| calculate ∫_0 ^∞ ((x^2 ln(x))/((1+x)^4 ))dx |
| calculate ∫_0 ^∞ ((x^2 lnx)/((1+x^2 )^3 ))dx |
| ∫e^x tanx dx |
| (√(bemath)) ∫ (dx/( ((4−((3−2x))^(1/(3 )) ))^(1/(4 )) )) ? |
| (1)∫_e ^e^e ((ln (x).ln (ln (x)))/x) dx ? (2)lim_(x→π/4) ((cosec^2 x−2)/(cot x−1)) (3) Given { ((xy=((16y−9x)/(45)))),(((4/( (√x)))−(3/( (√y))) = 5)) :} ⇒find 9(√(xy)) |
| ∫((sin(x))/(x^2 +1))dx |
| lim_(n→∞) (1+Σ_(r=1) ^n (1/(3^r r!))Π_(k=1) ^r (2k−1)) |
| please evaluate : Ω=∫_0 ^( (1/2)) ((ln^2 (1−x))/x) dx=??? M.N.July 1970# .... Good luck.... |
| Please integrate ∫_0 ^1 (1/(1+x^c ))dx where c is a constant. |
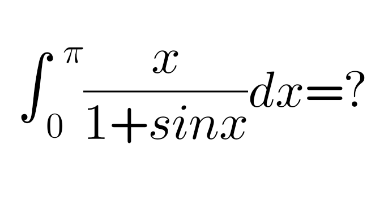
|
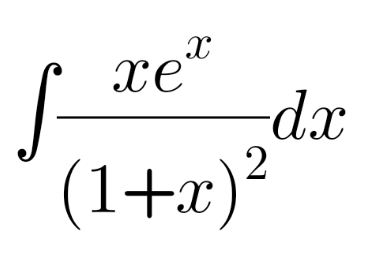
|

|
| ....calculus.... please solve : Ω_1 =∫_0 ^( (π/4)) ((√(tan(x))) +(√(cot(x))) )dx=?? Ω_2 =∫_0 ^(π/4) tan(x)ln((1+tan^2 (x)))dx =?? ...M.N.july 1970#... Good luck |
| calculate U_n =∫_([(1/n),n[^2 ) (x^2 −y^2 )e^(−x^2 −y^2 ) dxdy and lim_(n→+∞) U_n |
Pg 136 Pg 137 Pg 138 Pg 139 Pg 140 Pg 141 Pg 142 Pg 143 Pg 144 Pg 145 |