
Question and Answers Forum
IntegrationQuestion and Answers: Page 142









Pg 137 Pg 138 Pg 139 Pg 140 Pg 141 Pg 142 Pg 143 Pg 144 Pg 145 Pg 146
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 142 |
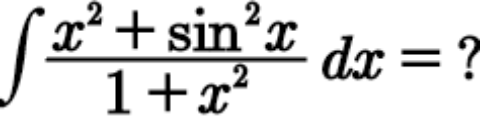
|
| ∫_(0 ) ^(π/4) ln(tanx+1)dx |

|

|
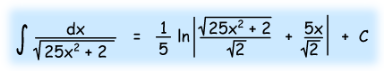
|
| find ∫_0 ^1 (√(1+x^4 ))dx |
| If f(x) continue in [ 1,30] and ∫_6 ^(30) f(x)dx = 30, then ∫_1 ^9 f(3y+3)dy = __ |

|
| ((bemath)/(Σ_(i=cooll) ^(nice) (joss)_i )) ∫ ((x^2 dx)/( (√(x^2 +25)))) |
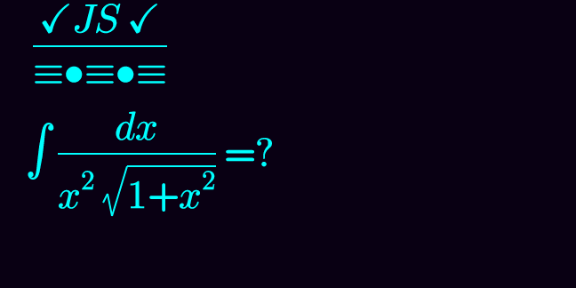
|

|

|

|

|

|

|
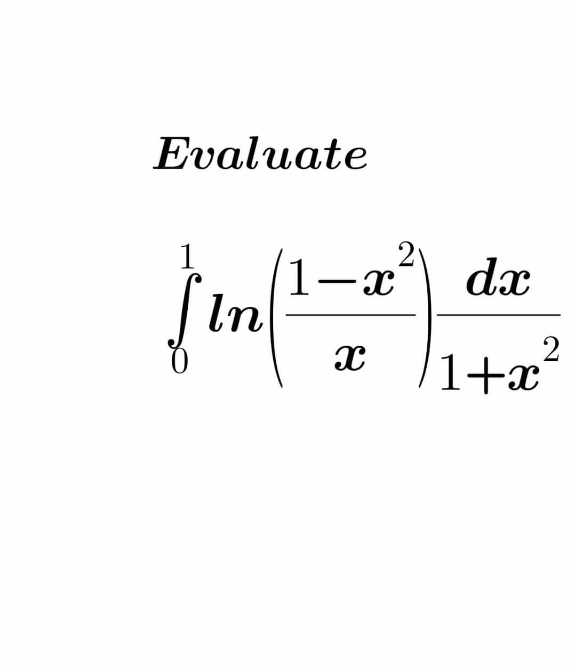
|
| calculate I_n =∫_0 ^(2π) ((cos(nx))/(cosx +sinx))dx (n→natural) |
| let f(x) =((sin(αx))/(sinx)) , 2π periodi even developp f at fourier serie |
| calculate ∫_0 ^∞ ((arctan(2+2t^2 ))/(1+t^2 ))dt |
| calculate ∫_0 ^1 ((ln(1+(√(1+x^2 ))))/(√(1+x^2 )))dx |
| calculateA_n = ∫_0 ^∞ (dx/((x^2 +n)(x^2 +2n))) with n integr natural≥1 |
| calculate ∫_0 ^π ((sin(nx))/(cosx))dx with n integr |
| ∫_0 ^(1/2) ((ln(1-t)ln(t))/t) dt I′m about to give up |
| ∫_0 ^(π/2) ((ln (cos x)ln (sin x))/(tan x)) dx |
| Given a function f(x+3)=f(x) for ∀x∈R. If ∫_(−3) ^6 f(x)dx = −6 then ∫_3 ^9 f(x) dx = ? |
Pg 137 Pg 138 Pg 139 Pg 140 Pg 141 Pg 142 Pg 143 Pg 144 Pg 145 Pg 146 |