
Question and Answers Forum
IntegrationQuestion and Answers: Page 145



Pg 140 Pg 141 Pg 142 Pg 143 Pg 144 Pg 145 Pg 146 Pg 147 Pg 148 Pg 149
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 145 |
| find ∫_0 ^1 ((arctan(2x))/(1+x^2 ))dx |
| f integrable continue on [a,b] let m =inf f(x) and M=sup f(x) (x ∈[a,b] prove that (b−a)^2 ≤∫_a ^b f(x)dx×∫_a ^b (dx/(f(x)))≤(((b−a)^2 )/4)(((m+M)^2 )/(mM)) |
| ♣ Question♣ Why ??? ....∫_0 ^( (π/2)) (√((((2^x −1)sin^3 (x))/((2^x +1)(sin^3 (x)+cos^3 (x)))) ))<(π/8) ....M.N.... |
| ⊚bemath⊚ ∫ x^6 (√(1−x^2 )) dx ? |
| ⊞bemath⊞ ∫ ((sin x)/(sin^3 x+cos^3 x)) dx ? |
| ⊵JS⊴ ∫ _0 ^( π/6) sin^2 (6x) cos^4 (3x) dx ? [ by using the Gamma function ] |
| ∫_0 ^4 ((ln x)/(√(4x−x^2 ))) dx ? |
| @bemath@ ∫_0 ^2 x ((8−x^3 ))^(1/3) dx =? |

|
| ∫(x^3 +x^6 )(((x^3 +2))^(1/3) )dx |

|
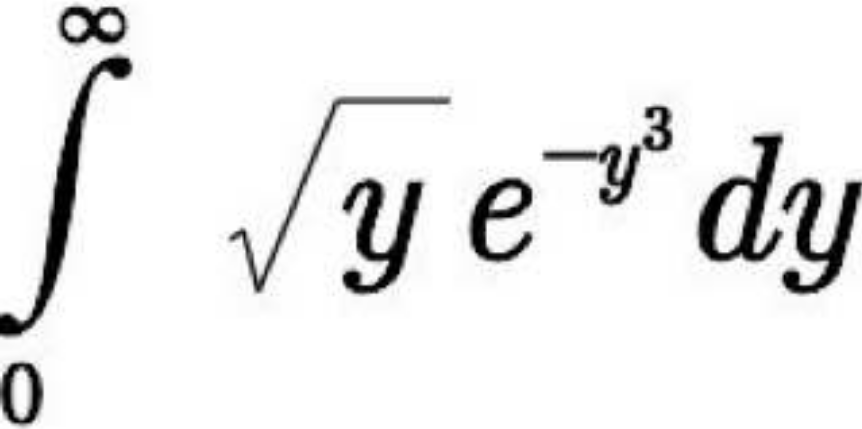
|
| ∫ (((√(1+x^2 )) dx)/x^4 ) ? |
| ∫_0 ^π ((cosx)/(√(2−sin^2 x)))dx |
| ∫_0 ^π ((sec^2 x)/(√(1−tan^2 x)))dx |
| let f(a) =∫_0 ^π (dx/(a+cos^2 x)) with a>0 1) explicite f(a) 2)explicite g(a) =∫_0 ^π (dx/((a+cos^2 x)^2 )) 3) find tbe valued of intevrsls ∫_0 ^π (dx/(1+cos^2 x)) and ∫_0 ^π (dx/((1+cos^2 x)^2 )) |
| ∫_0 ^π ((cosx)/(2+sin^2 x))dx |
| ∫_0 ^π (x/(1+cos^2 x))dx |

|
| calculate ∫_0 ^∞ ((tsin(2t))/(t^2 +4)) dt |
| ∀n∈(0, 1)∀x∈R : f(x) = (n/(n−1))x+n The given function gives a linear line that goes through points (0, n) and (1−n, 0). The function changes as n changes. What area is beneath the shape made as n goes from 0→1? |
| ∫(( dx)/((√(x^3 )) ^3 (√(1 +^4 (√x^3 ))))) = ? |
| ∫e^(2x) sine^x dx=?? |
| ∫tan(lnx)dx=??? |
| ∫sin(ln3x)dx=??? |
| ∫2xdx |
Pg 140 Pg 141 Pg 142 Pg 143 Pg 144 Pg 145 Pg 146 Pg 147 Pg 148 Pg 149 |