
Question and Answers Forum
IntegrationQuestion and Answers: Page 150
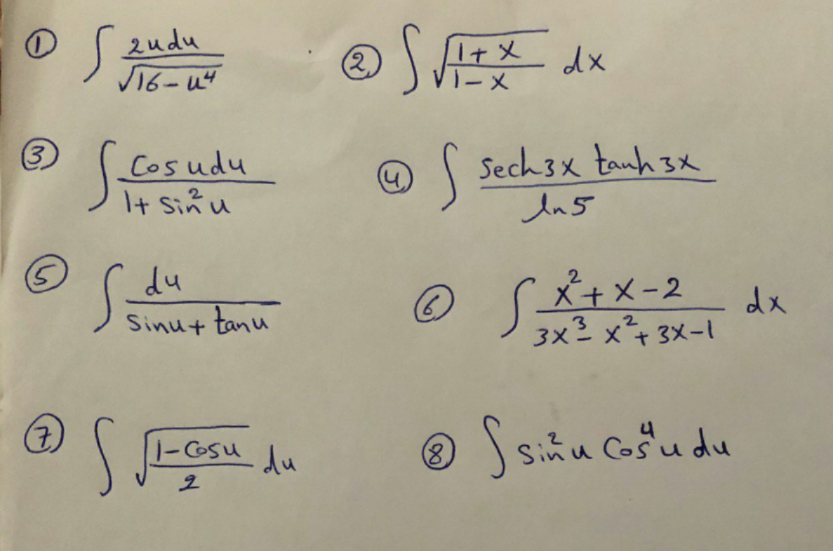
Pg 145 Pg 146 Pg 147 Pg 148 Pg 149 Pg 150 Pg 151 Pg 152 Pg 153 Pg 154
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 150 |
| calculate ∫_(−∞) ^(+∞) (dx/((x^2 −x+1)(x^2 +3)^2 )) |
| ∫_0 ^1 ((x^(98) −99x+98)/(logx))dx |
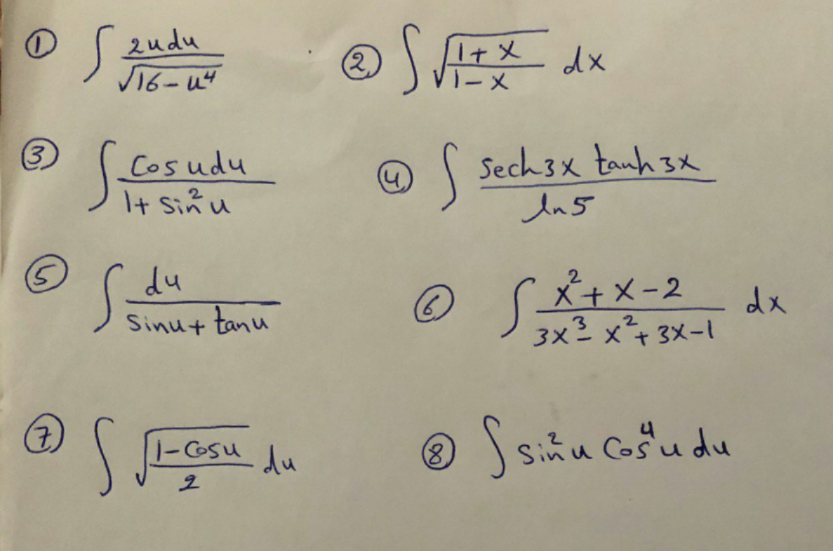
|
| find ∫ (dx/(cos^4 x)) |
| ∫(dx/(x^(1/3) +2)) |
| ∫ (dx/((1−sinx)^2 )) ? |
| ∫_c ((x^2 +2xy^2 )dx+(x^2 y^2 −1)dy) where C is the boundary of region define by y^2 = 4x and y =1 ? |
| calculate ∫_0 ^∞ (dx/((2x+1)^4 (x+3)^5 )) |
| calculate ∫_0 ^∞ ((arctan(ch(x)))/(x^2 +9))dx |
| Solve for n, such that; 1−(1/2)+∙∙∙+(((−1)^n )/(n+1))=∫_0 ^1 (x^(n+1) /(1+x))dx−ln2−(−1)^(n+1) |
| ∫_0 ^1 tan^(−1) (((2x−1)/(1+x−x^2 )))dx |
| what is the value of ∫_c (x+2y)dx+(4−2x)dy around the ellipse C: (x^2 /(16))+(y^2 /8)=1 in the counterclockwise direction ? |
| calculate ∫_(−∞) ^∞ (dx/((x^2 +x +1)^2 (2x^2 +5)^2 )) |
| calculate ∫_3 ^(+∞) (dx/((x^2 −1)^3 (x+2)^2 )) |
| ∫_0 ^∞ ((cosx)/(x^2 +1))dx |
| given f(x) = f(x+(π/6)) ∀x∈R if ∫_0 ^(π/6) f(x)dx = T then ∫_π ^(7π/3) f(x+π) dx ? |
| ∫ ((x dx)/((cot x+tan x)^2 )) = (a) (x/(16))−((x sin 4x)/(32))−((cos 4x)/(128))+c (b) (x/(16))+((x sin 4x)/(32))−((cos 4x)/(128))+c (c) (x/(16))+((xsin 4x)/(64))+((cos 4x)/(128))+c (d)(x/(16))+((xcos 4x)/(32))+((sin 4x)/(128))+c |
| ∫ (dx/((√x) ((x)^(1/4) +1))) =__ (a) −((9 (x)^(1/4) +1)/(18((x)^(1/4) +1)^9 )) + c (b) ((9 (x)^(1/4) +1)/(18((x)^(1/4) +1)^9 )) +c (c) −((9 (x)^(1/4) −1)/(18((x)^(1/4) +1)^9 )) +c (d) ((9 (x)^(1/4) +1)/(8((x)^(1/4) +1)^9 )) + c |
| ∫(x/((a^2 cosx+b^2 sinx)))dx |
| ∫ (x^2 +2x^4 +3x^6 )(√(1+x^2 +x^4 )) dx |
| I(n)=∫_0 ^∞ ((ln x)/(cosh^n x ))dx is there a simpler way to calculat those values |
| ∫_0 ^1 x^(−x) dx |
| ∫_0 ^∞ (1/((1+x^2 )^6 )) dx ? |
| ∫x^(−x) dx |
| ∫_0 ^∞ (x^3 /(e^x +1))dx |
| ∫_0 ^1 sin(logx)dx |
Pg 145 Pg 146 Pg 147 Pg 148 Pg 149 Pg 150 Pg 151 Pg 152 Pg 153 Pg 154 |