
Question and Answers Forum
IntegrationQuestion and Answers: Page 151
Pg 146 Pg 147 Pg 148 Pg 149 Pg 150 Pg 151 Pg 152 Pg 153 Pg 154 Pg 155
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 151 |
| given 5x+12y = 60 min value of (√(x^2 +y^2 )) |
| lim_(x→0) ((x^2 sin (x^(−4) ))/x) ? |
| ∫ (dθ/(2sin^2 θ−cos^2 θ)) ? |
| ∫ (dx/(x^3 +3x−5)) ? |
| ∫(e^x /((1+x^2 )^2 ))∙(x^3 −x^2 +x+1)dx |
| ∫ ((sin(x))/x) dx |
| I=2∫_0 ^(1/(√2)) ((sin^(−1) (x))/x) dx −∫_0 ^1 ((tan^(−1) (x))/x)dx |
| I=2∫_0 ^(1/(√2)) ((sin^(−1) (x))/x) dx −∫_0 ^1 ((tan^(−1) (x))/x) dx |
| ∫ (√(x+(√(x+(√(x+(√(x+(√(x+...)))))))))) dx |
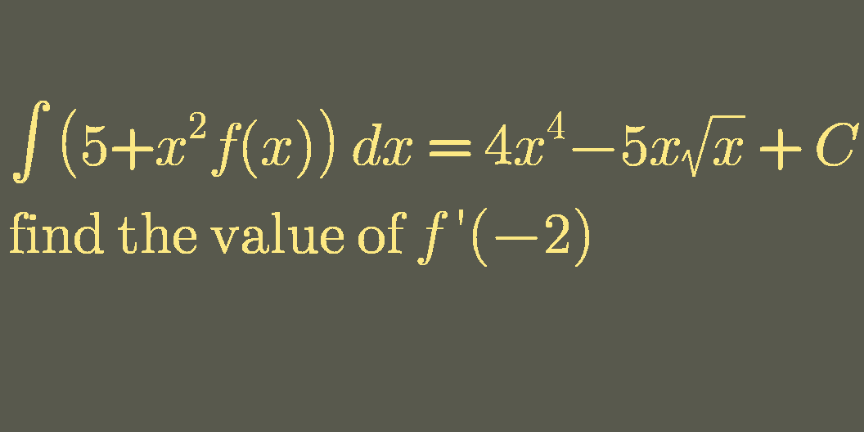
|
| (1)∫(1/(cos (√x))) dx (2) ∫ (1/(2+cot x)) dx (3) ∫ (1/(ln(cos x))) dx |
| what is the volume of region bounded by y =x^2 −2x and y=x that is rotated about y=4 ? |
| ∫(dx/(x^(10) +x^2 )) |
| Calculate ; J=∫(dx/(x(x^2 +x−1)^2 )) K=∫((x^3 +x−1)/((x^2 +2)^2 ))dx L=∫(dx/(x+(√(x^2 +1)))) |
| ∫_0 ^1 ((x^(98) −99x+98)/(logx))dx |
| calculate ∫_0 ^∞ e^(−x) ln(1+e^x )dx |
| calculate ∫_0 ^1 e^(−x) ln(1+e^x )dx |
| ∫ln(x−(√x)+1)dx |
| ∫(x/(sin^2 x−3)) |
| ∫((x(√6)sec^2 (x/2))/(1+9tan^4 (x/2)+18tan^2 (x/2)))dx |
| find the area bounded inner the curve r = 4−2cos θ and outer the curve r = 6+2cos θ |
| ∫((xdx)/((1+x^2 )(√(1−x^2 )))) |
| ∫_0 ^(π/2) ((cos x)/(1+cos x+sin x)) dx ? |
| ∫ ((1+csc 2x)/(1−sin 2x)) dx ? |
| Do this integration(please do it step by step and write the used formula) ∫(1/2)(sin x)(e^(sin x) )dx |
| ∫_1 ^2 ln(((x^4 + 4)/(x^2 + 4)))(dx/x) |
Pg 146 Pg 147 Pg 148 Pg 149 Pg 150 Pg 151 Pg 152 Pg 153 Pg 154 Pg 155 |