
Question and Answers Forum
IntegrationQuestion and Answers: Page 188

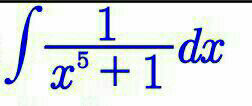


Pg 183 Pg 184 Pg 185 Pg 186 Pg 187 Pg 188 Pg 189 Pg 190 Pg 191 Pg 192
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 188 |
| Evaluate using cauchy′s integral ∫_c (e^(iπ) /((z^2 +4)^2 (z+1)^2 ))dz where c is a circle with ∣z−i∣=3.5 help please |
| ∫ _0 ^( 1) ((sin (ln x))/(ln (x))) dx |

|
| find f(x) if f ′(x) + f(x^2 ) = 2x+1 |
| ∫((z+2)/z) |
| let ϕ(x)=Γ(x).Γ(1−x) find ∫_(1/3) ^(1/2) ln(ϕ(x))dx |
| find ∫ (x^2 −1)(√(x^2 +1))dx |
| 1)find ∫ ln((√x)+(√(x+1)))dx 2) calculate ∫_0 ^1 ln((√x)+(√(x+1)))dx |
| 1) find f(a) =∫_0 ^∞ (dx/(x^4 +a)) with a>0 2) find g(a)=∫_0 ^∞ (dx/((x^4 +a)^2 )) 3) find value of integrals ∫_0 ^∞ (dx/(x^4 +1)) ,∫_0 ^∞ (dx/(2x^4 +8)) ∫_0 ^∞ (dx/((x^4 +1)^2 )) and ∫_0 ^∞ (dx/((2x^4 +8)^2 )) |
| calculate U_n = ∫_(−(1/n)) ^(1/n) x^2 (√((1−x)/(1+x)))dx (n integr and n≥2) 2) find nature of Σ U_n |
| ∫_0 ^1 ((1+x^4 )/(1+x^3 +x^7 )) dx |
| ∫_(−π) ^π x^(2020) (sin x+cos x) dx = 8 find ∫_(−π) ^π x^(2020) cos x dx = ? |
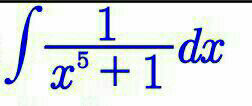
|
| calculate ∫_0 ^∞ (x^n /(sh(x)))dx with n integr natural |

|
| ∫ (2−x^2 )^3 dx = |
| show that ∫_0 ^(+∞) (1/(x^4 +2x^2 cos(((2π)/5))+1)) dx=(π/(2φ)) |
| ∫_0 ^x sinh(x−t) cosh(t) dt |

|
| e^(∫((2dx)/(xlnx))) |
| show that lim_(n→∞) ∫_0 ^1 ...∫_0 ^1 (n/(x_1 +x_2 +x_3 +...+x_n ))dx_1 dx_2 ...dx_n =2 |
| ∫((sin(7x))/(cos(3x))) dx |
| ∫_0 ^π ln(((1+b cos(x))/(1+a sin(x)))) dx −1<a<b<1 |
| ∫(x/((x^2 +1)^(3/2) arctan(x))) dx |
| ∫ (dx/((16+9sin x)^2 )) |
| calculate ∫_(−∞) ^(+∞) ((arctan(2x^2 ))/(1+x^2 ))dx |
Pg 183 Pg 184 Pg 185 Pg 186 Pg 187 Pg 188 Pg 189 Pg 190 Pg 191 Pg 192 |