
Question and Answers Forum
IntegrationQuestion and Answers: Page 195



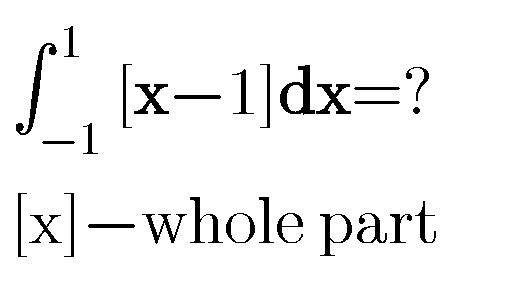

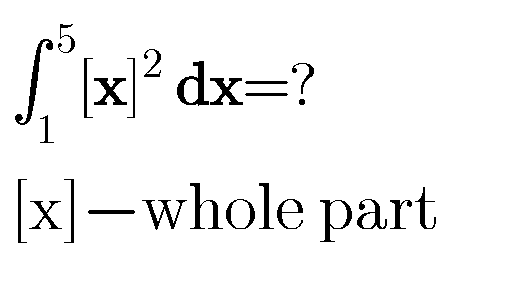
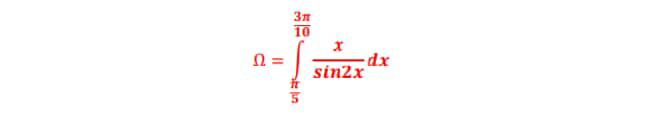
Pg 190 Pg 191 Pg 192 Pg 193 Pg 194 Pg 195 Pg 196 Pg 197 Pg 198 Pg 199
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 195 |

|

|
| how to prove ∫_0 ^1 x^n (1−x)^(m ) dx = ((m! ×n!)/((m+n)!)) via Gamma function |
| ∫ e^(sin 2x) .cos x dx = |
| ∫e^(√(sin x)) dx=? |
| Convergence of I=∫_0 ^( ∞) (e^t /(e^(−t) +e^(2t) ∣sint∣))dt |

|
| For witch value of α the integral I=∫_0 ^∞ ((1/(√(1+2x^2 )))−(α/(1+x)))dx converge; and in this case calculate α |
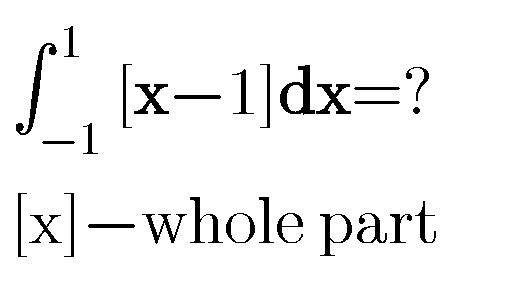
|
| ∫_( 0) ^( 1) (√(x^3 + 1)) dx |

|
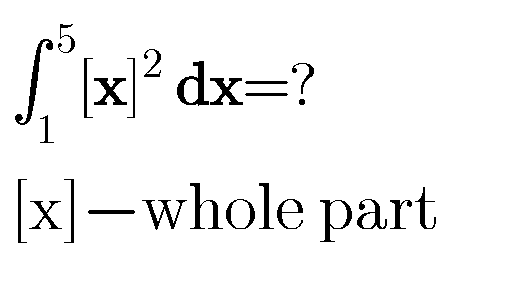
|
| calculate ∫_0 ^π {cos^8 x +sin^8 x}dx |
| find value of ∫_0 ^1 ln(1+ix^2 )dx and ∫_0 ^1 ln(1−ix^2 )dx with i=(√(−1)) |
| I) For witch value of α the integral C=∫_0 ^( ∞) ((1/(√(1+2x^2 )))−(1/(x+1)))dx conveege ? And in this case calculate α. II) Let Δ={(x; y)/ ∣x∣+∣y∣≤2} a) Calculate I_1 = ∫∫_Δ dxdy and ∫∫_Δ ((dxdy)/((∣x∣+∣y∣)^2 +4)) |
| calculate A_n =∫_0 ^1 cos(narcosx)dx with n integr natural |
| find ∫_0 ^1 ln(1+x^4 )dx |
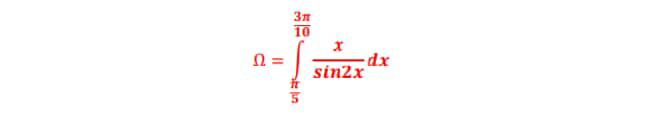
|
| 1) expicite f(x)=∫_0 ^1 ((ln(1+xt^2 ))/(1+t^2 ))dt with x≥0 2)calculate ∫_0 ^1 ((ln(1+t^2 ))/(1+t^2 ))dt and ∫_0 ^1 ((ln(1+2t^2 ))/(1+t^2 ))dt |
| prove that with using hypergeometric function ∫_0 ^π sin(x^2 )=(π^3 /3) 1F_2 [(3/4);(3/2);(7/4);((−π^4 )/4)] |
| Solve this ∫_ (((x−yz))/((x^2 +y^2 −2xyz)^(3/2) ))dz |
| does this matter reasonable ∫ sin^x (x) dx ? |
| ∫ (dx/((√(x ))((x)^(1/(4 )) +1)^(10) )) = ? |
| ∫^1 _0 ((ln((1/x)+x))/(x^2 +1))dx ? |
| find ∫_0 ^∞ e^(−x^3 ) cos(x^2 )dx |
| find ∫_0 ^∞ e^(−x^3 ) dx |
Pg 190 Pg 191 Pg 192 Pg 193 Pg 194 Pg 195 Pg 196 Pg 197 Pg 198 Pg 199 |