
Question and Answers Forum
IntegrationQuestion and Answers: Page 196

Pg 191 Pg 192 Pg 193 Pg 194 Pg 195 Pg 196 Pg 197 Pg 198 Pg 199 Pg 200
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 196 |
| Solve this ∫_ (((x−yz))/((x^2 +y^2 −2xyz)^(3/2) ))dz |
| does this matter reasonable ∫ sin^x (x) dx ? |
| ∫ (dx/((√(x ))((x)^(1/(4 )) +1)^(10) )) = ? |
| ∫^1 _0 ((ln((1/x)+x))/(x^2 +1))dx ? |
| find ∫_0 ^∞ e^(−x^3 ) cos(x^2 )dx |
| find ∫_0 ^∞ e^(−x^3 ) dx |
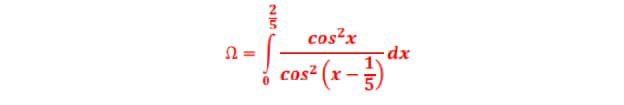
|

|
| ∫(cot^2 x+cot^4 x)dx |
| ∫(tan^2 x+tan^4 x)dx |
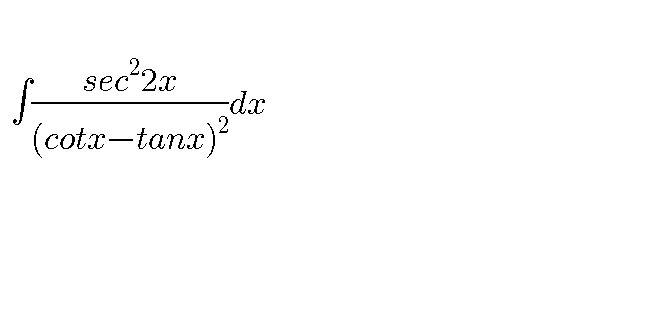
|
| find ∫_0 ^∞ e^(−(x^3 +(1/x^3 ))) dx |
| ∫(dx/(1−(√(cos(x))))) |
| Convergence of : 1) I=∫_1 ^( ∞) ((e^(−t/5) ∣sin(lnt)∣)/((t−1)^(3/2) ))dt 2) I=∫_1 ^∞ ((√(lnx))/((x−1)(√x)))dx |
| ∫_0 ^1 (x^n /(Σ_(k=0) ^(n−1) x^k ))dx=? |
| ∫_0 ^π ((cos (nx)−cos (nα))/(cos (x)−cos (α))) dx |
| ∫_(−1) ^1 ((cos (x))/(1+e^(1/x) )) dx ? |
| Find out ∫_0 ^1 ln(1−t+t^2 )dt Then deduce the value of A=Σ_(n=1) ^∞ (1/(n(n+1) (((2n+1)),(n) ))) |
| calculate ∫_0 ^∞ (((−1)^x^2 )/((x^2 −x+1)^3 ))dx |
| calculate ∫_0 ^∞ ((ln(x))/((1+x)^3 ))dx |
| find A_n =∫_0 ^∞ ((sin(x)sin(2x)....sin(nx))/x^n )dx with n≥2 integr |
| find I_(a,b) =∫_0 ^∞ ((sin(ax)sin(bx))/x^2 )dx witha>0 and b>0 |
| find f(λ) =∫_0 ^∞ e^(−λx^2 ) ch(x^2 +λ)dx with λ>0 |
| find ∫_(−∞) ^(+∞) ((e^(−x^2 ) arctan(x^2 +1))/(x^2 +1))dx |
| calculate ∫_0 ^∞ ((e^(−x^2 ) arctan(x))/x)dx |
| if:∫cos(f(x))dx=g(x) ∫sin(f(x))dx=? (use g(x)) |
Pg 191 Pg 192 Pg 193 Pg 194 Pg 195 Pg 196 Pg 197 Pg 198 Pg 199 Pg 200 |