Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 206

Question Number 73397 Answers: 1 Comments: 1

find f(x)=∫_0 ^1 e^(−t) ln(1−xt^2 )dt with ∣x∣<1 2)calculate ∫_0 ^1 e^(−t) ln(1−(t^2 /2))dt

$f i n d f (x) = \int_{0}^{1} e^{- t} l n (1 - {x t}^{2}) d t w i t h ∣ x ∣< 1$ $2) c a l c u l a t e \int_{0}^{1} e^{- t} l n (1 - \frac{t^{2}}{2}) d t$

Question Number 73338 Answers: 0 Comments: 1

calculate ∫_0 ^∞ ((arctan(2cosx))/(3+x^2 ))dx

$c a l c u l a t e \int_{0}^{\infty} \frac{a r c t a n (2 c o s x)}{3 + x^{2}} d x$

Question Number 73337 Answers: 0 Comments: 3

calculate ∫_0 ^∞ ((cos(artan(2x)))/((3+x^2 )^2 ))dx

$c a l c u l a t e \int_{0}^{\infty} \frac{c o s (a r t a n (2 x))}{{(3 + x^{2})}^{2}} d x$

Question Number 73336 Answers: 1 Comments: 1

find ∫_0 ^∞ e^(−t) ln(1+e^t )dt

$f i n d \int_{0}^{\infty} e^{- t} l n (1 + e^{t}) d t$

Question Number 73335 Answers: 1 Comments: 2

eplcit f(x)=∫_0 ^1 ln(x+t+t^2 )dt with x>(1/4) 2)calculate ∫_0 ^1 ln(t^2 +t +(√2))dt

$e p l c i t f (x) = \int_{0}^{1} l n (x + t + t^{2}) d t w i t h x > \frac{1}{4}$ $2) c a l c u l a t e \int_{0}^{1} l n (t^{2} + t + \sqrt{2}) d t$

Question Number 73333 Answers: 0 Comments: 1

calculate ∫_0 ^∞ ((cos(π +2x^2 ))/((x^2 +4)^2 ))dx

$c a l c u l a t e \int_{0}^{\infty} \frac{c o s (π + 2 x^{2})}{{(x^{2} + 4)}^{2}} d x$

Question Number 73331 Answers: 0 Comments: 1

calculate ∫_0 ^∞ ((ln(1+e^(−3x^2 ) ))/(3+x^2 ))dx

$c a l c u l a t e \int_{0}^{\infty} \frac{l n (1 + e^{- 3 x^{2}})}{3 + x^{2}} d x$

Question Number 73293 Answers: 2 Comments: 2

Explicit f(x)= ∫_1 ^∞ ((lnt)/((x^2 +t^2 )^2 )) dt

$E x p l i c i t f (x) = \int_{1}^{\infty} \frac{l n t}{{(x^{2} + t^{2})}^{2}} d t$

Question Number 73279 Answers: 1 Comments: 0

Question Number 73275 Answers: 0 Comments: 2

∫(4/(x^2 (√(4−xδϰ)))) ?

$\int \frac{4}{x^{2} \sqrt{4 - x δ ϰ}} ?$

Question Number 73238 Answers: 1 Comments: 1

let 0<a<1 calculate ∫_0 ^∞ ((ln(t)t^(a−1) )/(1+t))dt and ∫_0 ^∞ ((ln^2 (t)t^(a−1) )/(1+t))dt

$l e t 0 < a < 1 c a l c u l a t e \int_{0}^{\infty} \frac{l n (t) t^{a - 1}}{1 + t} d t a n d \int_{0}^{\infty} \frac{{l n}^{2} (t) t^{a - 1}}{1 + t} d t$

Question Number 73231 Answers: 1 Comments: 1

find the sum of Σ_(n=0) ^∞ (n^2 −3n+1)e^(−n)

$f i n d t h e s u m o f \sum_{n = 0}^{\infty} (n^{2} - 3 n + 1) e^{- n}$

Question Number 73230 Answers: 0 Comments: 0

calculate A_n =∫_0 ^∞ ((1+x^n )/(2+x^(2n) ))dx and J_n =∫_0 ^∞ ((2+x^(3n) )/(5+x^(7n) ))dx with n integr natural not 0

$c a l c u l a t e A_{n} = \int_{0}^{\infty} \frac{1 + x^{n}}{2 + x^{2 n}} d x a n d J_{n} = \int_{0}^{\infty} \frac{2 + x^{3 n}}{5 + x^{7 n}} d x$ $w i t h n i n t e g r n a t u r a l n o t 0$

Question Number 73225 Answers: 0 Comments: 0

calculate f(x)=∫_0 ^π ln(x^2 −2xcosθ +1)dθ with x real.

$c a l c u l a t e f (x) = \int_{0}^{π} l n (x^{2} - 2 x c o s θ + 1) d θ w i t h x r e a l .$

Question Number 73202 Answers: 2 Comments: 3

∫((2x^2 −1+2x(√(x^2 −1)))/(x^2 −x+(x−1)(√(x^2 −1))))dx=? ∫(dx/(x(√(x+1))(√((1−x)^3 ))))=?

$\int \frac{2 x^{2} - 1 + 2 x \sqrt{x^{2} - 1}}{x^{2} - x + (x - 1) \sqrt{x^{2} - 1}} d x = ?$ $\int \frac{d x}{x \sqrt{x + 1} \sqrt{{(1 - x)}^{3}}} = ?$

Question Number 73258 Answers: 1 Comments: 0

Question Number 73182 Answers: 0 Comments: 3

calculate ∫_0 ^∞ xe^(−x^2 ) arctan(x−(1/x))dx

$c a l c u l a t e \int_{0}^{\infty} {x e}^{- x^{2}} a r c t a n (x - \frac{1}{x}) d x$

Question Number 73181 Answers: 1 Comments: 1

calculate ∫_1 ^(3 ) ((x−2)/(√(x^2 +x+1)))dx

$c a l c u l a t e \int_{1}^{3} \frac{x - 2}{\sqrt{x^{2} + x + 1}} d x$

Question Number 73180 Answers: 0 Comments: 0

calculate ∫_0 ^∞ ((lnx)/((x+1)^3 ))dx

$c a l c u l a t e \int_{0}^{\infty} \frac{l n x}{{(x + 1)}^{3}} d x$

Question Number 73179 Answers: 1 Comments: 1

caoculate ∫_0 ^∞ ((arctan(x^2 −1))/(2x^2 +1))dx

$c a o c u l a t e \int_{0}^{\infty} \frac{a r c t a n (x^{2} - 1)}{2 x^{2} + 1} d x$

Question Number 73178 Answers: 1 Comments: 0

calculate ∫_0 ^∞ ((ln(2+x^2 ))/(x^2 −x+1))dx

$c a l c u l a t e \int_{0}^{\infty} \frac{l n (2 + x^{2})}{x^{2} - x + 1} d x$

Question Number 73155 Answers: 0 Comments: 0

reposting a former question... ∫(((x)^(1/5) −1)/((√x)+1))dx= [t=(x)^(1/(10)) → dx=10(x^9 )^(1/(10)) dx] =10∫((t^9 (t−1))/(t^4 −t^3 +t^2 −t+1))dt= =10∫(t^6 −t^4 −t)dt+10∫((t(t^2 −t+1))/(t^4 −t^3 +t^2 −t+1))dt= =((10)/7)t^7 −2t^5 −5t^2 +(5+(√5))∫(t/(t^2 −((1−(√5))/3)t+1))dt+(5−(√5))∫(t/(t^2 −((1+(√5))/2)t+1))dt= and it′s easy to solve these

$reposting a former question . . .$ $\int \frac{\sqrt[5]{x} - 1}{\sqrt{x} + 1} d x =$ $[t = \sqrt[10]{x} \to d x = 10 \sqrt[10]{x^{9}} d x]$ $= 10 \int \frac{t^{9} (t - 1)}{t^{4} - t^{3} + t^{2} - t + 1} d t =$ $= 10 \int (t^{6} - t^{4} - t) d t + 10 \int \frac{t (t^{2} - t + 1)}{t^{4} - t^{3} + t^{2} - t + 1} d t =$ $= \frac{10}{7} t^{7} - 2 t^{5} - 5 t^{2} + (5 + \sqrt{5}) \int \frac{t}{t^{2} - \frac{1 - \sqrt{5}}{3} t + 1} d t + (5 - \sqrt{5}) \int \frac{t}{t^{2} - \frac{1 + \sqrt{5}}{2} t + 1} d t =$ $and {it}^{'} s easy to solve these$

Question Number 73147 Answers: 1 Comments: 1

∫((x−6)/(x^3 +1))dx

$\int \frac{x - 6}{x^{3} + 1} d x$

Question Number 73144 Answers: 1 Comments: 1

calculte ∫ ((x+(√(2+x^2 )))/(x+1−(√(2+x^2 ))))dx

$c a l c u l t e \int \frac{x + \sqrt{2 + x^{2}}}{x + 1 - \sqrt{2 + x^{2}}} d x$

Question Number 73037 Answers: 1 Comments: 1

Question Number 72988 Answers: 1 Comments: 1

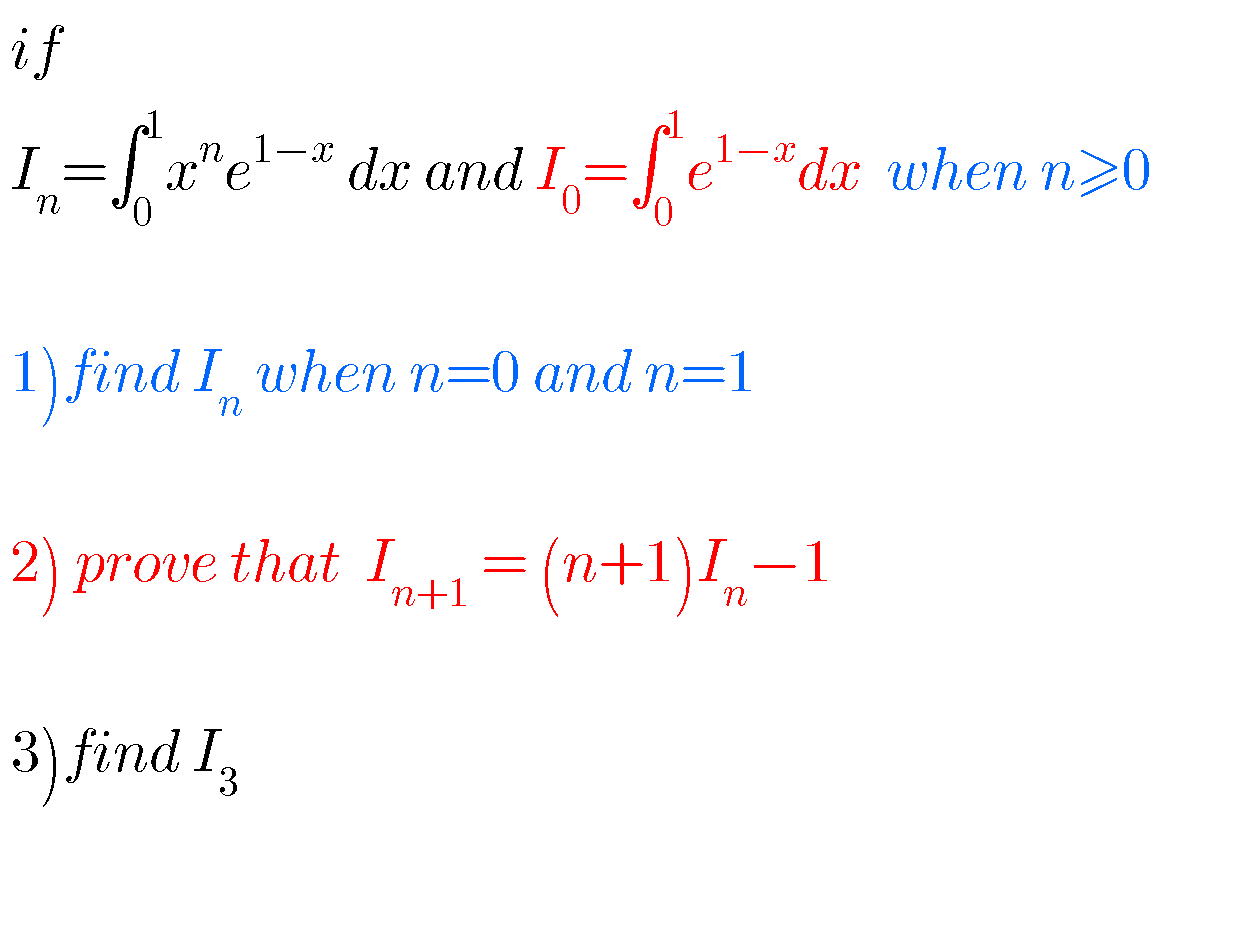
calculate f(x)=∫_0 ^∞ (e^(−xt^2 ) /(4+t^2 ))dt with x>0

$c a l c u l a t e f (x) = \int_{0}^{\infty} \frac{e^{- {x t}^{2}}}{4 + t^{2}} d t w i t h x > 0$

Pg 201 Pg 202 Pg 203 Pg 204 Pg 205 Pg 206 Pg 207 Pg 208 Pg 209 Pg 210

Terms of Service

Contact: info@tinkutara.com