
Question and Answers Forum
IntegrationQuestion and Answers: Page 212


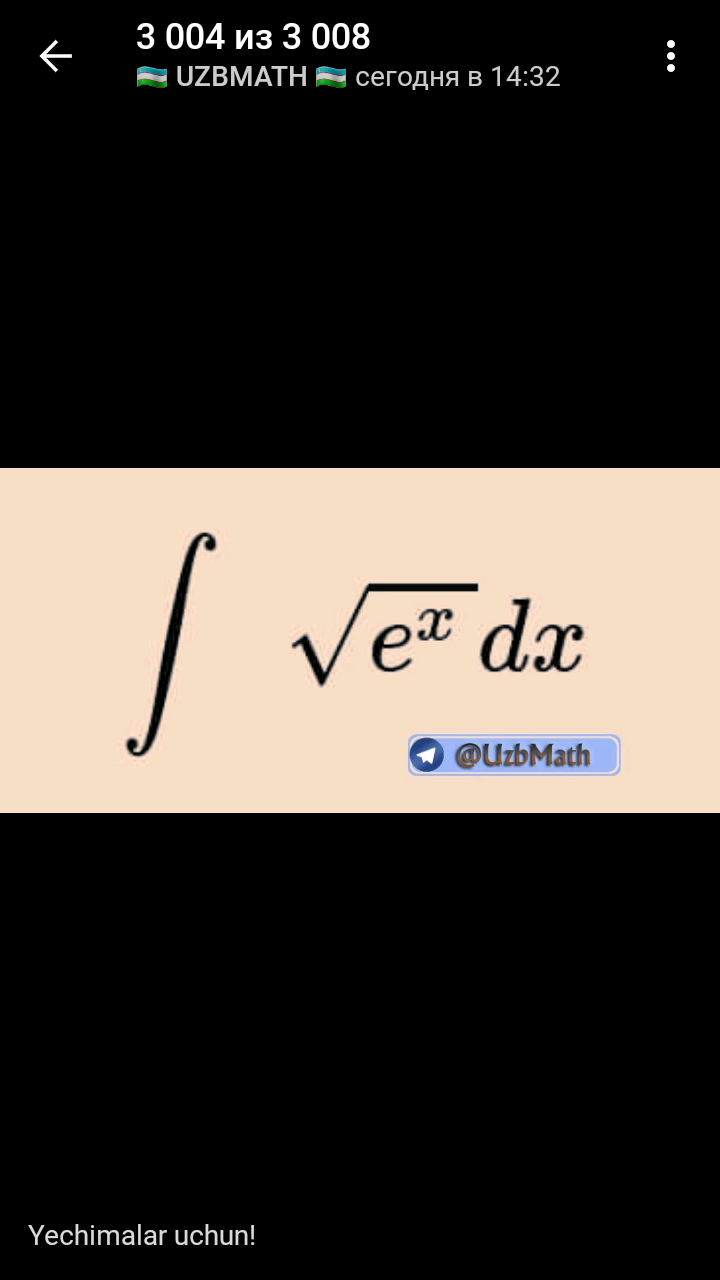
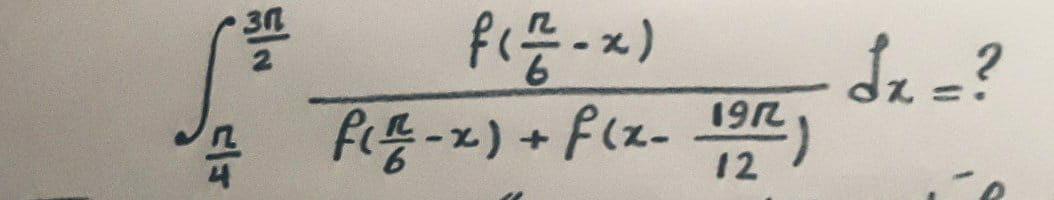

Pg 207 Pg 208 Pg 209 Pg 210 Pg 211 Pg 212 Pg 213 Pg 214 Pg 215 Pg 216
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 212 |
| Let consider (a_n )_n and (u_n )_n two reals sequence defined such as a_0 =1 , ∀ n>1 a_(n+1) =Σ_(p=0) ^n a_p a_(n−p) and Σ_(p=0) ^n a_p u_(n−p) =0 Part1 1)Express ∀ n >1 a_n in terms of n 2) Find the largest domain of convergence of the integer serie {a_n x^n } 3)Determinate ∀ x∈D the sum f(x) of {a_n x^n } 4)Find the radius of convergence of the serie {u_n x^n } 5) Give the relation that between the sum S(x) of the second serie and (x/(f(x))) 6) Can you developp in integer serie g(x)=((πx)/(tan(πx))) Part2 Now do the part 1 but in the order 2)−1)−3)−4)−5)−6) |
| Explicit f(a)=Σ_(n=1) ^∞ (((−1)^n )/(n(an+1))) |
| Find the arc length, given the curve x(t) = sin (πt), y(t) = t , 0 ≤ t ≤ 1 |
| the 2 formulas for solving ∫(dx/(x^3 +px+q)) with “nasty” solutions of x^3 +px+q=0 with p, q ∈R case 1 D=(p^3 /(27))+(q^2 /4)>0 ⇒ x^3 +px+q=0 has got 1 real and 2 conjugated complex solutions u=((−(q/2)+(√((p^3 /(27))+(q^2 /4)))))^(1/3) ∧v=((−(q/2)−p(√((p^3 /(27))+(q^2 /4)))))^(1/3) x_1 =u+v x_2 =(−(1/2)+((√3)/2)i)u+(−(1/2)−((√3)/2)i)v x_3 =(−(1/2)−((√3)/2)i)u+(−(1/2)+((√3)/2)i)v α=u+v∧β=((√3)/2)(u−v) ⇔ u=(α/2)+(β/(√3))∧v=(α/2)−(β/(√3)) x_1 =α x_2 =−(α/2)+βi x_3 =−(α/2)−βi ∫(dx/(x^3 +px+q))=∫(dx/((x−α)(x^2 +αx+((α^2 +4β^2 )/4))))= =(1/(9α^2 +4β^2 ))(∫(dx/((x−α)))−∫((x+2α)/(x^2 +αx+((α^2 +4β^2 )/4)))dx)= =(1/(9α^2 +4β^2 ))(ln ∣x−α∣ −(1/2)ln ((2x+α)^2 +4β^2 ) −((3α)/(2β))arctan ((2x+α)/(2β))) +C ...now calculate the constants case 2 D=(p^3 /(27))+(q^2 /4)<0 ⇒ x^3 +px+q=0 has got 3 real solutions x_k =(2/3)(√(−3p)) sin (((2π)/3)k+(1/3)arcsin ((3(√3)q)/(2(√(−p^3 ))))) with k=0, 1, 2 let x_1 =α, x_2 =β, x_3 =γ ∫(dx/(x^3 +px+q))=∫(dx/((x−α)(x−β)(x−γ)))= =(1/((α−β)(α−γ)))∫(dx/(x−α))+(1/((β−α)(β−γ)))∫(dx/(x−β))+(1/((γ−α)(γ−β)))∫(dx/(x−γ))= =((ln ∣x−α∣)/((α−β)(α−γ)))+((ln ∣x−β∣)/((β−α)(β−γ)))+((ln ∣x−γ∣)/((γ−α)(γ−β)))+C ...now calculate the constants |
| ∫(dx/(sin2x−sec(x))) |
| Find K=∫_0 ^1 ((ln(1−t+t^2 ))/t) dt |
| ∫(√x)/1+((x ))^(1/3) dx |
| ∫dx/(((π+e)^x^2 ))^(1/x) |

|
| find f(a) =∫_1 ^2 arctan(x+(a/x))dx and calculate f^′ (a) at form of integral |
| find ∫ arctan(x+(1/x))dx |
| calculate ∫_0 ^∞ ((arctan(x^2 −1))/(x^2 +4))dx |
| find ∫ ((x^2 dx)/((x^3 −8)(x^4 +1))) |
| find ∫ (dx/(1+sinx +sin(2x))) |

|
| ∫(√(e^y^2 )) dy pleas sir can you help me? |
| ∫e^(y^2 /2) dy |
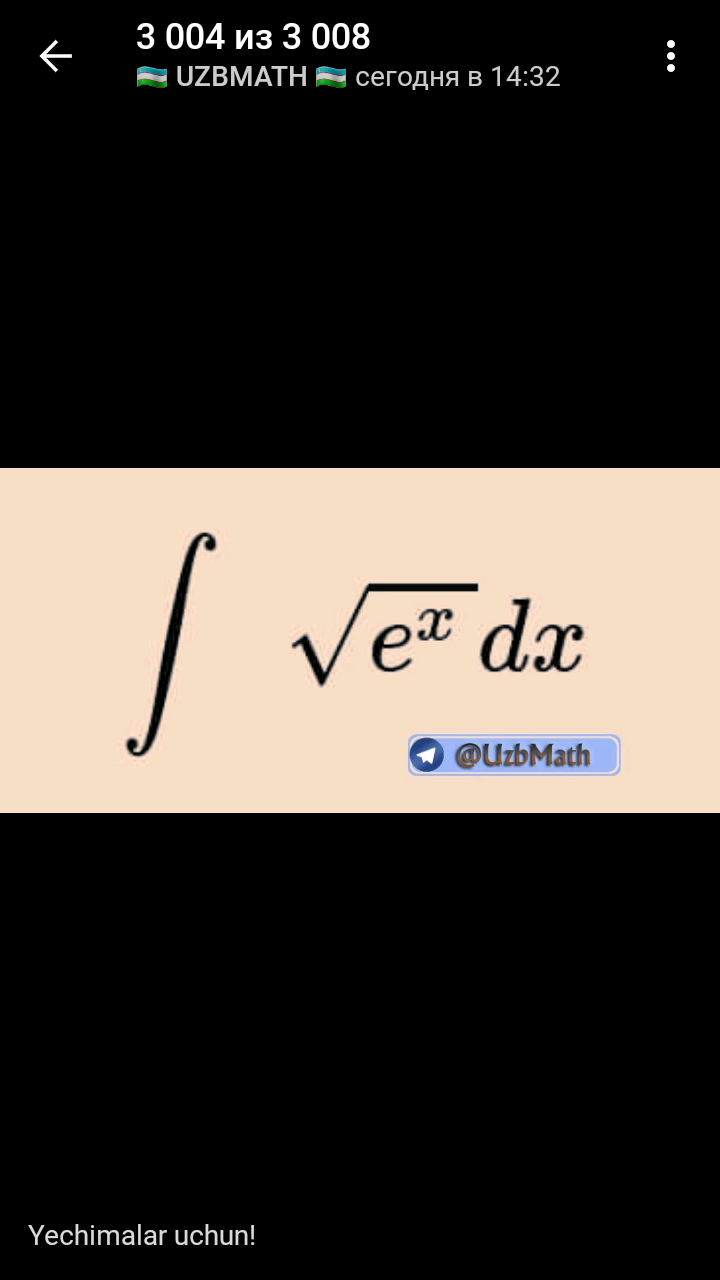
|
| let A(θ) = ∫_0 ^∞ (dx/((x^2 +3)(x^4 −e^(iθ) ))) with 0<θ<(π/2) 1) calculate A(θ) interms of θ 2) determine also ∫_0 ^∞ (dx/((x^2 +3)(x^4 −e^(iθ) )^2 )) |
| let A_n =∫_0 ^(π/4) x^n {1+cosx +cos(2x)}^2 dx find a relation of recurrence betwedn the A_n |
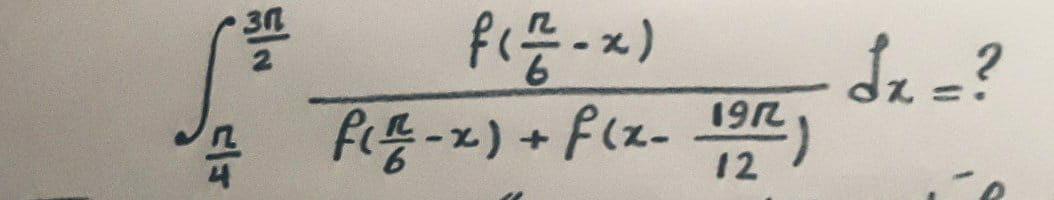
|
| ∫e^(y^2 /2) dy |

|
| find ∫ (dx/(x^2 −z)) with z from C . |
| calculate ∫_(−∞) ^(+∞) (dx/(x^2 −z)) with z from C |
| ∫_0 ^2 x(8−x^3 )^(1/3) dx |
Pg 207 Pg 208 Pg 209 Pg 210 Pg 211 Pg 212 Pg 213 Pg 214 Pg 215 Pg 216 |