
Question and Answers Forum
IntegrationQuestion and Answers: Page 219


Pg 214 Pg 215 Pg 216 Pg 217 Pg 218 Pg 219 Pg 220 Pg 221 Pg 222 Pg 223
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 219 |
| find the values of ∫_0 ^∞ cos(x^2 )dx and ∫_0 ^∞ sin(x^2 )dx(fresnel integrals) by using Γ(z) =∫_0 ^∞ t^(z−1) e^(−t) dt |
| prove without calculus that ∫_0 ^∞ cos(x^2 )dx=∫_0 ^∞ sin(x^2 )dx |
| find ∫_0 ^∞ e^(−x^3 ) sin(x^3 )dx |
| ∫ ((√((1+x^2 )))/x^2 ) dx = ? |
| calculate ∫_0 ^1 ((arctan((√(x^2 +2))))/((x^2 +1)(√(x^2 +2))))dx |
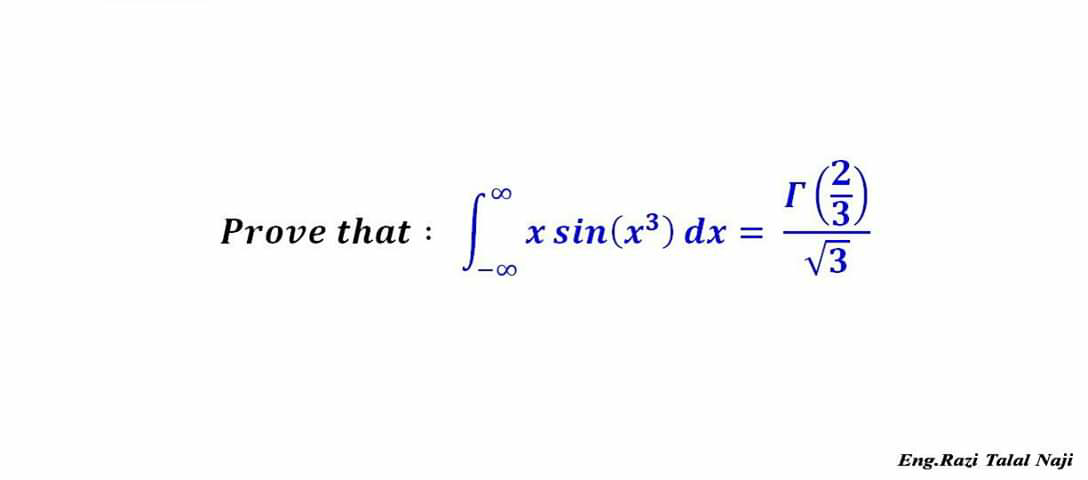
|
| find the value of U_n =∫_(−∞) ^(+∞) e^(−nx^2 ) sin(x^2 −2x)dx find nature of the serie Σ U_n and Σe^(−n^2 ) U_n |
| find the value of ∫_(−∞) ^(+∞) cos(x^2 −x+1)dx |
| let f(x) =∫_0 ^1 (dt/(ch(t)+xsh(t))) 1) find a explicit form of f(x) 2) determine g(x) =∫_0 ^1 (dt/((ch(t)+xsh(t))^2 )) 3) calculate ∫_0 ^1 (dt/(ch(t)+3sh(t))) and ∫_0 ^1 (dt/({ch(t)+3sh(t)}^2 )) |
| let f(x) =∫_0 ^(π/4) (dt/(x+tant)) with x real 1) find aexplicit form of f(x) 2)find also g(x) =∫_0 ^(π/4) (dt/((x+tant)^2 )) 3)give f^((n)) (x)at form of integral 4)calculate ∫_0 ^(π/4) (dt/(2+tant)) and ∫_0 ^(π/4) (dt/((2+tant)^2 )) |
| ∫(x/(√(ln(1/x)))) dx |

|
| ∫dx/x^2 −x+1 |

|
| ∫_0 ^( π/2) tan^3 xdx = ? |
| pls i need solution plssss...asap n lim ∈ ((r^3 /(r^4 +n^4 ))) n→∞ r=1 please try and understand the way i typed it |
| find ∫_0 ^∞ e^(−x) ln(1+x^2 )dx |
| calculate ∫_0 ^1 e^(−2t) ln(1−t)dt |
| calculate ∫_(−(π/6)) ^(π/6) (x/(sinx))dx |
| calculate ∫_0 ^∞ ((1−cos(2x^2 ))/x^2 )dx |
| calculate ∫_0 ^∞ ((sin(3x^2 ))/x^2 )dx |
| fnd ∫ (dx/(x+2−(√(3+x^2 )))) |
| find ∫ (dx/(x(√(x+1)) +(x+1)(√x))) 2) calculate ∫_1 ^(√3) (dx/(x(√(x+1)) +(x+1)(√x))) |
| Calculate lim_(a−>∞) ∫_0 ^∞ (dx/(1+x^a )) |
| 1) calculate ∫_(−∞) ^∞ (dx/(1+ix)) and ∫_(−∞) ^∞ (dx/(1−ix)) 2)deduce the value of ∫_(−∞) ^∞ (dx/(1+x^2 )) 3)calculate ∫_(−∞) ^∞ (dx/(1+ix^2 )) and ∫_(−∞) ^∞ (dx/(1−ix^2 )) 4)deduce the value of ∫_(−∞) ^∞ (dx/(1+x^4 )) |
| ∀ x, y >0 B(x,y)=∫_0 ^1 t^(x−1) (1−t)^(y−1) dt Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt 1) show that ∀ x>0 Γ(x+1)=xΓ(x) and lim_(n−>∞) ((x(x+1)......(x+n))/(n^x n!))=(1/(Γ(x))) and deduce that lim_(n−>∞) ((Γ(x+n))/(n^x Γ(n)))=1 b) Prove that if a function f satisfies f(x+1)=xf(x) et lim_(n−>∞) ((f(x+n))/(n^x f(n)))=1 then ∀ x>0 f(x)= f(1)Γ(x) 3) Show that B(x+1, y)=(x/(x+y))B(x,y) B(1,x)=(1/x) 2) Now let consider ∀ y f(x)=((B(x,y)Γ(x+y))/(Γ(y))) Show that f verify the same property as Γ ( just the both proved up ) 3) Deduce that ∀ x,y>0 B(x,y)=((Γ(x)Γ(y))/(Γ(x+y))) |
Pg 214 Pg 215 Pg 216 Pg 217 Pg 218 Pg 219 Pg 220 Pg 221 Pg 222 Pg 223 |