
Question and Answers Forum
IntegrationQuestion and Answers: Page 222
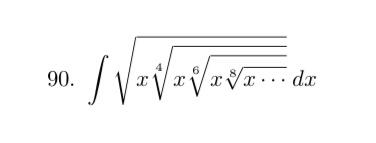

Pg 217 Pg 218 Pg 219 Pg 220 Pg 221 Pg 222 Pg 223 Pg 224 Pg 225 Pg 226
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 222 |
| ∫(((√(x+1)) − (√(x−1)))/((√(x+1)) + (√(x−1)))) dx |
| let U_n = ∫_(1/n) ^(2/n) Γ(x)Γ(1−x)dx with n≥3 1) calculate and determine lim_(n→+∞) U_n 2) study the convergence of Σ U_n |
| find ∫_0 ^∞ (dx/(Γ(x))) with Γ(x) =∫_0 ^∞ t^(x−1) e^(−t) dt (x>0) |
| ∫(√(tanh(x))) dx |
| let f(a) =∫_0 ^∞ ((cos(x^2 )−sin(x^2 ))/((x^2 +a^2 )^2 ))dx with a>0 1) calculate f(a) 2) find the values of ∫_0 ^∞ ((cos(x^2 )−sin(x^2 ))/((x^2 +1)^2 )) and ∫_0 ^∞ ((cos(x^2 )−sin(x^2 ))/((x^2 +3)^2 ))dx . |
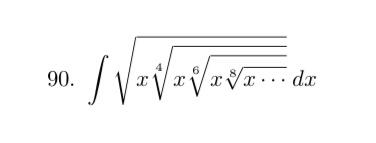
|
| let f(a)=∫_0 ^∞ ((cos(x^2 ) +sin(x^2 ))/((x^2 +a^2 )^2 )) dx with a>0 1) calculate f(a) 2) find the values of ∫_0 ^∞ ((cos(x^2 )+sin(x^2 ))/((x^2 +1)^2 ))dx and ∫_0 ^∞ ((cos(x^2 )+sin(x^2 ))/((x^2 +3)^2 ))dx |
| ∫log (tan x)dx |
| calculate ∫_1 ^2 ∫_0 ^x (1/((x^2 +y^2 )^(3/2) ))dydx |
| find ∫_1 ^(+∞) (dx/(x^2 (√(1+x+x^2 )))) |
| let A_λ =∫_0 ^π (dx/(λ +cosx +sinx)) (λ ∈ R) 1) find a explicit form of A_λ 2) find also B_λ =∫_0 ^π (dx/((λ +cosx +sinx)^2 )) 3) calculate ∫_0 ^π (dx/(2+cosx +sinx)) and ∫_0 ^π (dx/((3+cosx +sinx)^2 )) |
| find ∫ (dx/(1+cosx +cos(2x))) |
| ∫log(((1+sinhx))/((1−sinhx)))tanhx dx |
| ∫(cos^4 x+sin^4 x)/(cos2x+1)dx |
| ∫(cos^4 x+sin^4 x)/(cos2x+1)dx |
| Given that g(x)=(2/((1+x)(1+3x^2 )) a) express g(x) in partial fractions. b) evaluate ∫_0 ^1 g((x) dx. |
| ∫((ln(ln(x)))/((ln(x))^n )) dx , n≠1 |
| calculate ∫_0 ^1 ((sin(lnx))/(lnx))dx |
| let f(x) =∫_0 ^π (dt/(x+sint)) with xreal 1) find a explicit form of f(x) 2) find also g(x) =∫_0 ^π (dt/((x+sint)^2 )) 3) give f^((n)) (x) at form of integral 4) calculate ∫_0 ^π (dt/(3+sint)) and ∫_0 ^π (dt/((3+sint)^2 )) |
| ∫tanθ/1+^− sinθ dθ |
| ∫(secθtanθ)dθ/secθ+^− tanθ |

|
| let f(x) =∫_0 ^1 lnt ln(1−xt)dt with ∣x∣<1 1)determine a explicit form for f(x) 2) find also g(x) =∫_0 ^1 ((tlnt)/(1−xt))dt 3) give f^((n)) (x) at form of integral 4) calculate ∫_0 ^1 ln(t)ln(1−t)dt and ∫_0 ^1 ln(t)ln(2−t)dt 5) calculate ∫_0 ^1 ((tln(t))/(2−t)) dt . |
| ∫(dx/((x^8 +x^4 +1)^2 )) ∫_(1/x) ^x ((ln(t))/(t^2 +1)) dt |
| calculate ∫_0 ^(2π) ((cosθ)/(5+3cosθ))dθ |
| ∫(dx)/e^x +x |
Pg 217 Pg 218 Pg 219 Pg 220 Pg 221 Pg 222 Pg 223 Pg 224 Pg 225 Pg 226 |