
Question and Answers Forum
IntegrationQuestion and Answers: Page 225
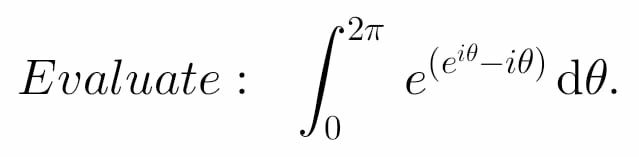
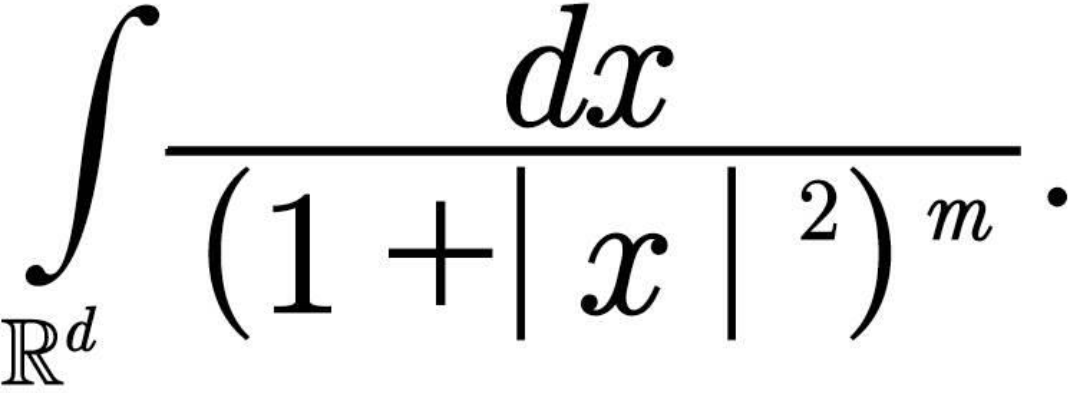
Pg 220 Pg 221 Pg 222 Pg 223 Pg 224 Pg 225 Pg 226 Pg 227 Pg 228 Pg 229
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 225 |
| ∫tan(1/x)dx |
| ∫tan(1/x)dx |
| ∫tan(1/x)dx |
| ∫tan(1/x)dx |
| ∫tan(1/x)dx |
| ∫tan(1/x)dx |
| calculate ∫_0 ^π ((tsint)/(3+sin^2 t)) dt |
| calculate ∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx |
| reduction formulas for n∈N, some n>0, some n>1 ∫sin^n x dx=−(1/n)cos x sin^(n−1) x +((n−1)/n)∫sin^(n−2) x dx ∫cos^n x dx=(1/n)sin x cos^(n−1) x +((n−1)/n)∫cos^(n−2) x dx ∫tan^n x dx=(1/(n−1))tan^(n−1) x −∫tan^(n−2) x dx ∫sec^n x dx=(1/(n−1))tan x sec^(n−2) x +((n−2)/(n−1))∫sec^(n−2) x dx ∫csc^n x dx=−(1/(n−1))cot x csc^(n−2) x +((n−2)/(n−1))∫csc^(n−2) x dx ∫cot^n x dx=−(1/(n−1))cot^(n−1) x −∫cot^(n−2) x dx |
| ∫secxdx ? |
| ∫_0 ^π (dx/((3+2cos x)^2 )) |
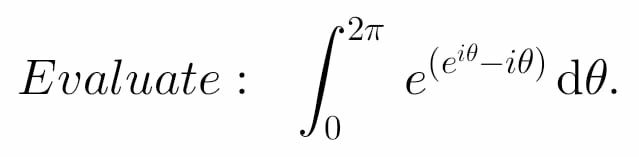
|
| calculate A=∫_0 ^∞ (x^(2017) /(1+x^(2019) )) dx and B =∫_0 ^∞ (x^(2019) /(1+x^(2021) )) dx calculate the fraction (A/B) |
| ∫e^x /Lnxdx |
| ∫ln(x)ln(1−x)ln(1−2x)dx |
| prove that ∫_0 ^1 arctan(x) cot(((πx)/2)) dx = ((3 ln^2 (2))/(2π))+((lnπ ln2)/π)+∫_0 ^∞ ((ln(1+x^2 ))/(e^(2πx) +1)) dx |
| ∫(1+4x+x^2 )^m dx |
| find ∫ (x^2 +1)(√((x+1)/(x−2)))dx |
| let f(a) =∫_(−∞) ^(+∞) (dx/((a^2 +x^2 )^3 )) with a>0 1) calculate f(a) 2)calculste also g(a) =∫_(−∞) ^(+∞) (dx/((a^2 +x^2 )^4 )) 3) find the values of integrals ∫_0 ^∞ (dx/((x^2 +1)^3 )) ∫_0 ^∞ (dx/((x^2 +2)^4 )) |
| calculate ∫_(−∞) ^(+∞) ((3x^2 −1)/(x^4 −2x^2 +3))dx |
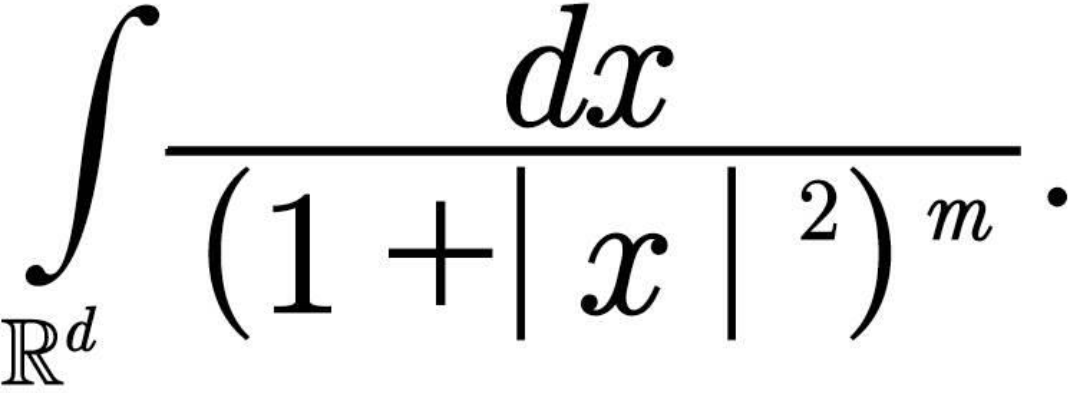
|
| useful formula ======== ∀a∈R^+ :∀b ∈R: a sin x +b cos x =(√(a^2 +b^2 ))sin (x+arctan (b/a)) ∫(dx/(a sin x +b cos x))= =(1/(√(a^2 +b^2 )))∫(dx/(sin (x+arctan (b/a))))= [t=x+arctan (b/a) → dx=dt] (1/(√(a^2 +b^2 )))∫(dt/(sin t))=−(1/(√(a^2 +b^2 )))ln ((1/(sin t))+(1/(tan t))) = =−(1/(√(a^2 +b^2 )))ln ∣(((√(a^2 +b^2 ))−b sin x +a cos x)/(a sin x +b cos x))∣ +C |
| 1) calculate ∫ (x^2 −x+2)(√(x^2 −x+1))dx 2)find the value of ∫_0 ^1 (x^2 −x+2)(√(x^2 −x +1))dx . |
| calculate ∫ (dx/(√((x−1)(2−x)))) |
| calculate ∫(√((x−3)(2−x)))dx |
| calculate ∫_0 ^π (dx/((√3)cosx +(√2)sinx)) |
Pg 220 Pg 221 Pg 222 Pg 223 Pg 224 Pg 225 Pg 226 Pg 227 Pg 228 Pg 229 |