
Question and Answers Forum
IntegrationQuestion and Answers: Page 231

Pg 226 Pg 227 Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 231 |
| 1) calculate f(x,y) =∫_0 ^∞ ((e^(−xt) cos(yt))/(√t)) dt and g(x,y) =∫_0 ^∞ ((e^(−xt) sin(yt))/(√t)) dt with x>0 and y>0 2) find the values of ∫_0 ^∞ ((e^(−2t) cos(t))/(√t)) dt and ∫_0 ^∞ ((e^(−t) cos(2t))/(√t)) dt |
| find the value of ∫_0 ^∞ (t^(a−1) /((1+t)^2 ))dt with 0<a<1 |
| ∫_0 ^∞ e^(−x^2 ) dx |
| ∫((2sin(x)+3cos(x))/(3sin(x)+4cos(x)))dx |
| find the value of I =∫_0 ^∞ ((e^(−t) sint)/(√t))dt and J =∫_0 ^∞ ((e^(−t) cos(t))/(√t))dt ,study first the convergence. |
| ∫ln(x+1)/(x^2 −x+1) limit ={ 0>2} |
| ∫(x^2 −4)^(1/2) dx trig substitution only |

|
| 1.∫(√(1+x+x^2 +x^3 ))dx=? 2.∫ ((√(1−tgx))/(sinx)) dx=? 3.∫ e^x .ln(1+(√(1+x^2 )))dx=? 4.∫ ((sinx)/(1+sinx+sin2x)) dx=? |
| let f(x) =∫_0 ^∞ (t^2 /(x^6 +t^6 )) dt with x>0 1) calculate f(x) 2) calculate g(x) =∫_0 ^∞ (t^2 /((x^6 +t^6 )^2 ))dt 3) find values of integrals ∫_0 ^∞ (t^2 /(t^6 +8))dt and ∫_0 ^∞ (t^2 /((t^6 +8)^2 ))dt . |
| calculate ∫∫∫_D e^(−x^2 −y^2 ) (√(x^2 +y^2 +z^2 ))dxdydz with D ={(x,y,z)∈R^3 / 0≤x≤1 , 1≤y≤2 and 2≤z≤3 } |
| find g(a) =∫(x+a)(√(x^2 −a^2 ))dx |
| find f(a) =∫ (x−a)(√(x^2 +a^2 ))dx |
| calculate ∫ ((x+3)/((x−2)(√(x^2 +x+1)))) dx |
| calculate ∫∫_([0,2]^2 ) ((arctan((√(x^2 +y^2 ))))/(3−(√(x^2 +y^2 ))))dxdy |
| calculate ∫∫_W e^(x−2y) sin(x+2y) dxdy W ={(x,y)^2 / 0≤x≤1 and 2≤y≤(√5)} |
| find ∫∫_([0,1]) ((x^2 −y^2 )/(3−(√(x^2 +y^2 )))) dxdy . |
| calculate ∫∫_([0,1]^2 ) (√(x^2 +y^2 ))sin((√(x^2 +y^2 )))dxdy |
| calculate ∫_0 ^∞ ((ln(2+e^(−t^2 ) ))/(t^2 +3))dt |
| calculate A_n =∫_(−∞) ^(+∞) (dx/((x^2 +x+1)^n )) with n integr natural(n≥1) |
| ∫(e^(3x^2 ) /((1−x^4 ))^(1/8) ) dx |
| ∫(dx/(sin3x+sin4x)) |
| ∫_( 0) ^( 2 (√(ln 3))) ∫_( (y/2)) ^( (√(ln 3))) e^x^2 dx dy |
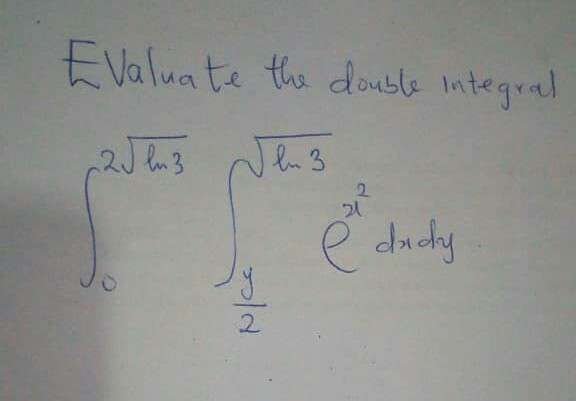
|
| calculate ∫ (√((x−1)/(x^2 +3)))dx . |
| calculate ∫_0 ^π ln(x^2 −2xsinθ +1)dθ |
Pg 226 Pg 227 Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 |