
Question and Answers Forum
IntegrationQuestion and Answers: Page 233

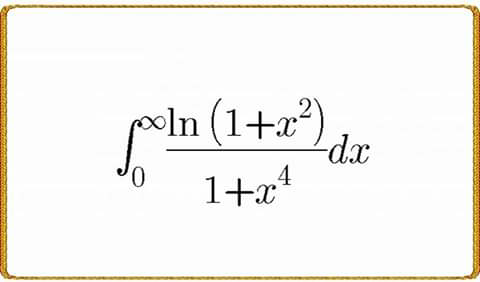
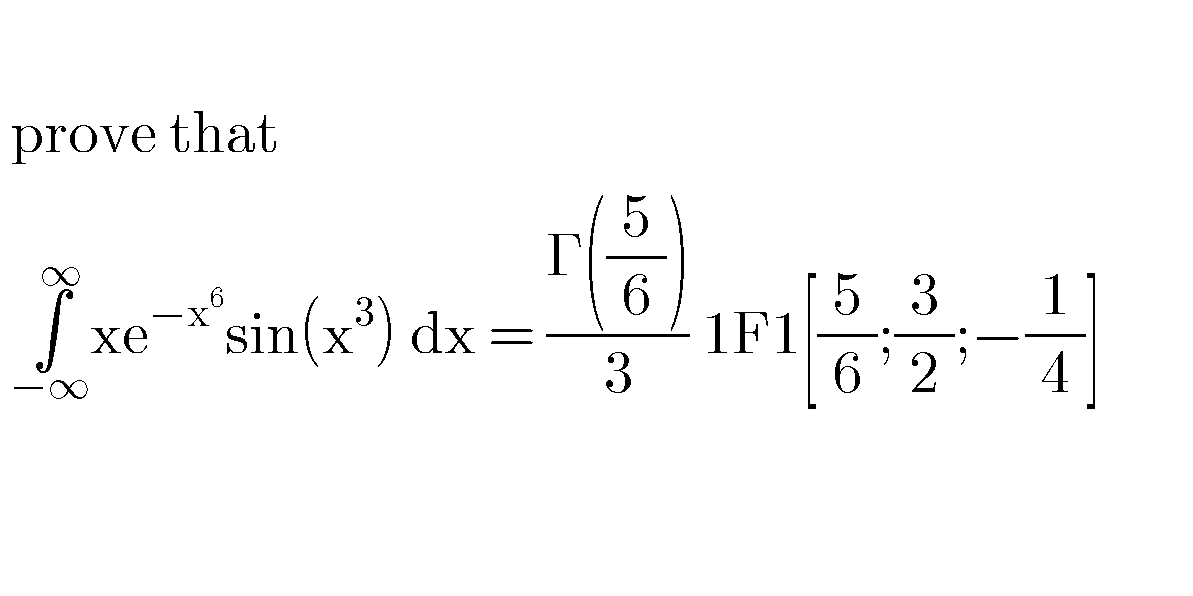
Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 233 |
| let f(a) =∫_0 ^1 ((sin(2x))/(1+ax^2 )) dx with ∣a∣<1 1) approximate f(a) by a polynom 2) find the value (perhaps not exact) of ∫_0 ^1 ((sin(2x))/(1+2x^2 )) dx 3) let g(a) = ∫_0 ^1 ((x^2 sin(2x))/((1+ax^2 )^2 )) dx approximat g(a) by a polynom 4) find the value of ∫_0 ^1 ((x^2 sin(2x))/((1+2x^2 )^2 )) dx . |
| find ∫_0 ^1 ((sinx)/(1+x^2 ))dx |
| ∫ ((x^(2 ) − 4)/((x^2 + 4)^2 )) dx |

|
| let U_n =∫_1 ^(+∞) (([nx]−[(n−1)x])/x^3 ) dx with n≥1 1) find U_n interms of n 2) find lim_(n→+∞) U_n 3) study the serie Σ_(n=1) ^∞ U_n |
| let f_n (a) =∫_0 ^a x^n (√(a^2 −x^2 ))dx with a>0 1) determine a explicit form of f(a) 2) let g_n (a) =f^′ (a) give g_n (a) at form of integral and give its value 3) find the value of ∫_0 ^2 x^3 (√(4−x^2 ))dx and ∫_0 ^(√3) x^4 (√(3−x^2 ))dx |
|
| ∫ ((x + sin(x))/(1 + cos(x))) dx |
| calculate I =∫_0 ^1 cos(2arctanx)dx and J =∫_0 ^1 sin(2arctanx)dx |
| calculate ∫_1 ^(+∞) (([2x]−[x])/x^4 ) dx |
| find ∫_0 ^1 arctan((2/(1+x)))dx |
| find Σ_(n=1) ^∞ (1/n^2 ) by use of integral ∫_0 ^(π/2) ln(2cosθ)dθ . |
| study the integral ∫_(−∞) ^(+∞) (1−cos((2/(x^2 +1))))dx |
| find ∫_(−∞) ^(+∞) tan((1/(1+x^2 )))dx |
| ∫(dx/((1+x^2 )^(3/2) )) solve this pls |
| ∫((csc^(2019) (x))/(sec^5 (x))) tan^2 (x) dx |
| find ∫ arctan((1/(1+x^2 )))dx |
| study the convergence of ∫_0 ^1 (((√(1+2x))−(√(1+x)))/(ln(1+x)))dx and determine its value. |
| calculate ∫_0 ^(π/2) (dx/((√2)cos^2 x +(√3)sin^2 x)) |
| ∫_(−π) ^π sin((1/(1−x^2 ))) dx |
| ∫(e^w /w^(n+1) )dw, n∈N |
| ∫(e^n /x^(n+1) )dx, n∈N |
| ∫_(−∞) ^∞ sin((1/(1+x^2 ))) dx |
| evaluate i.∫ (((x+1)/(x−1)))dx ii. ∫_0 ^π (2cosxsinx)dx iii. ∫_((π/(3 )) ) ^π (((sin2x)/(cos2x)))dx |
|
| calculate ∫_1 ^(+∞) ((ln(lnx))/(x^2 −x +1))dx |
Pg 228 Pg 229 Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 |