
Question and Answers Forum
IntegrationQuestion and Answers: Page 235

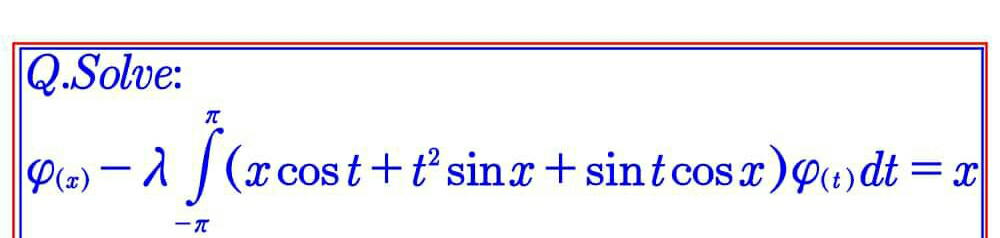


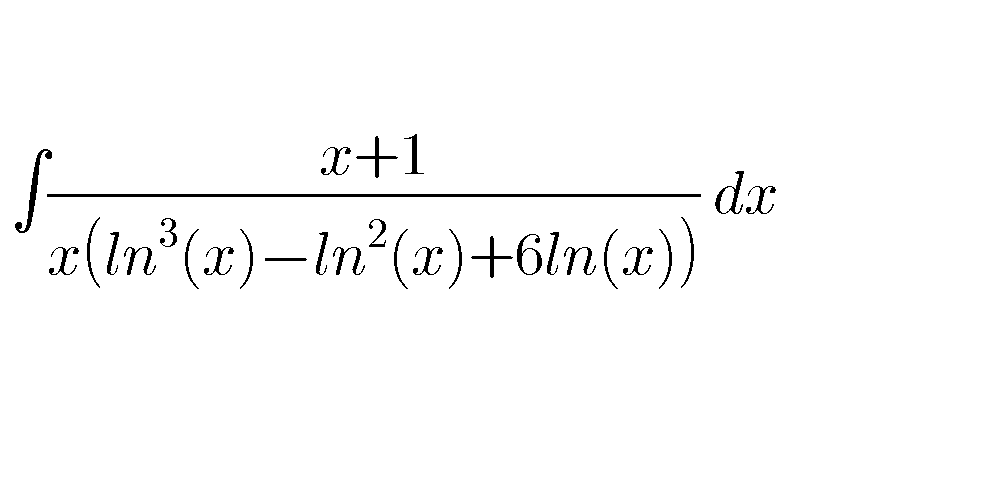

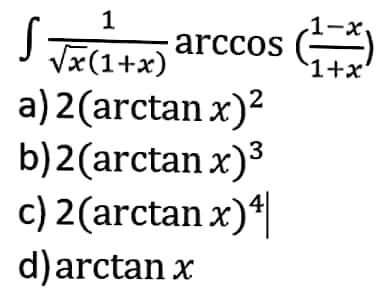
Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 235 |
| study the integral ∫_0 ^1 (x/(ln(1−x)))dx |
| calculate ∫_0 ^∞ ((ln(1+e^(−x^2 ) ))/(x^2 +4)) dx |
| calculate ∫_0 ^1 ((ln(1−x^2 ))/x) dx |

|
| ∫_0 ^(π/2) ln[((ln^2 (sin(x)))/(π^2 +ln^2 (sinx)))]((ln(cos(x)))/(tan(x)))dx |
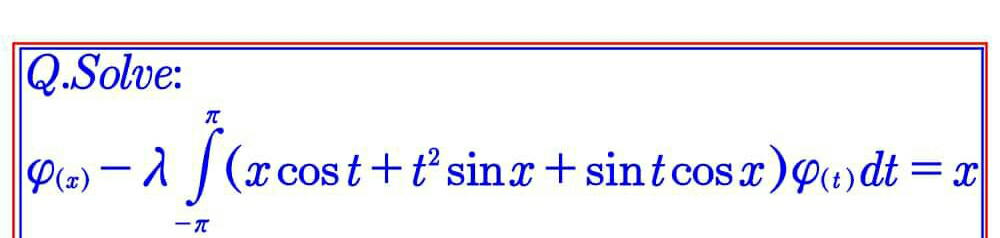
|
| find ∫_0 ^1 ln(x)ln(1−x^2 )dx |
| calculate ∫_0 ^1 ln(x)ln(1−x)ln(1−x^2 )dx |

|
| What are all intregal methods that exist like trigonometry sub. Gaussian method feyman method ? |
| if π is rational then there exists a I_n =(v^(2n) /(n!))∫_0 ^π x^n (x−π)^n sin(x)dx can someone give a easier way to expaned this |
| prove that∫_(−∞) ^∞ x^5 e^(−x^2 ) sin(x^3 ) dx=0.25474 |
| find ∫_0 ^1 ((ln^2 (x))/((1−x^2 )^2 ))dx |

|
| calculate ∫∫_W ((√(2x^2 +3y^2 ))/(x+y)) dxdy with W ={(x,y)∈R^2 / 0<x<1 and 0<y<1. |
| let f(t) =∫_0 ^3 (√(t +x +x^2 ))dx with t ≥(1/4) 1) find a explicit form of f(t) 2) find also g(t) = ∫_0 ^3 (dx/(√(t+x +x^2 ))) 3) calculate ∫_0 ^3 (√(1+x+x^2 ))dx , ∫_0 ^3 (√(2 +x+x^2 ))dx ∫_0 ^3 (dx/(√(2+x +x^2 ))) . |
| let f(a) =∫_0 ^1 ((ln^2 (x))/((1−ax)^2 )) dx with ∣a∣<1 1) find a explicit form of f(a) 2) determine A(θ) =∫_0 ^1 ((ln^2 (x))/((1−(cosθ)x)^2 ))dx with 0<θ<(π/2) |
| calculate ∫_0 ^1 ((lnx)/((1−x)^2 ))dx |
| find the value of ∫_0 ^1 ((ln(x))/((1−x^2 )^2 ))dx |
| find ∫ (√((√(2+x^2 ))−x))dx |
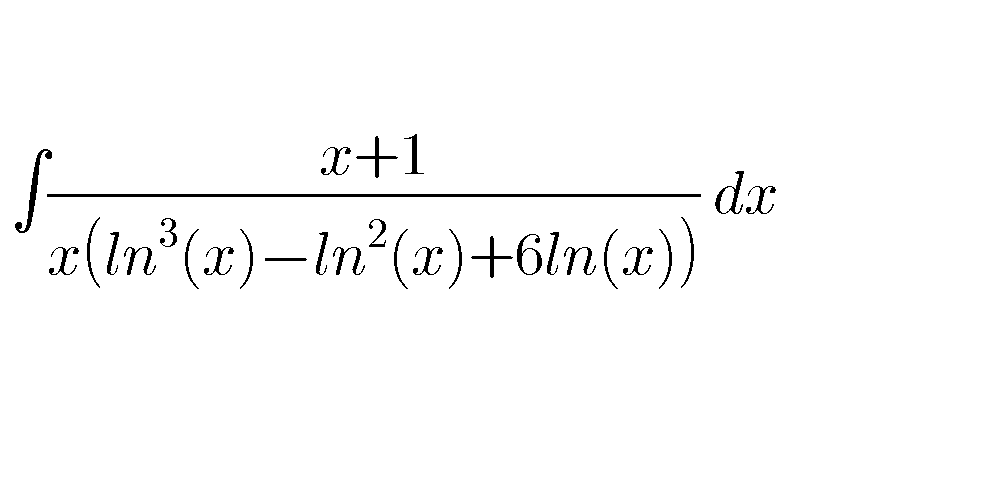
|
| let z ∈C and ∣z∣<1 find f(x)=∫_0 ^1 ln(1+zx)dx. |

|
| ∫e^(coth^(−1) (x)) dx |
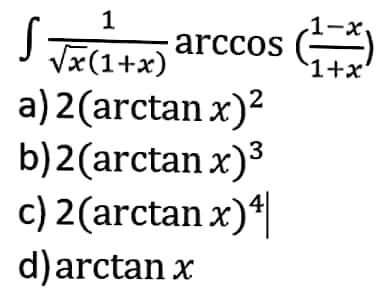
|
| find I_n = ∫ x^n arctan(x)dx with n integr natural. |
Pg 230 Pg 231 Pg 232 Pg 233 Pg 234 Pg 235 Pg 236 Pg 237 Pg 238 Pg 239 |