
Question and Answers Forum
IntegrationQuestion and Answers: Page 240


Pg 235 Pg 236 Pg 237 Pg 238 Pg 239 Pg 240 Pg 241 Pg 242 Pg 243 Pg 244
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 240 |
| find the value of ∫_0 ^∞ ((sin(x^2 ))/(x^4 +4))dx |
| 1) calculate I =∫_(−∞) ^(+∞) (dx/(x^2 −i)) and J =∫_(−∞) ^(+∞) (dx/(x^2 −i)) 2) find the value of ∫_(−∞) ^(+∞) (dx/(x^4 +1)) |
| ∫x(√(3x^3 +2)) dx=? |

|
| 1)calculate A_n =∫_(1/n) ^1 ((ln(1+x^2 ))/(1+x^2 ))dx with n integr and n≥1 2) find lim_(n→+∞) A_n 3) study the convergence of Σ A_n |
| let f(a) =∫_0 ^∞ (dx/(x^n +a^n )) with n integr ≥2 and a>0 1) calculate f(a) intems of a 2) let g(a) =∫_0 ^∞ (dx/((x^n +a^n )^2 )) calculate g(a) interms of a 3) find the values of integrals ∫_0 ^∞ (dx/(x^8 +16)) and ∫_0 ^∞ (dx/((x^8 +16)^2 )) |
| let f(x) =∫_0 ^∞ ((cos(xt))/(x^2 +t^2 )) dt with x>0 1) find f(x) 2) find the values of ∫_0 ^∞ ((cos(t))/(1+t^2 ))dt and ∫_0 ^∞ ((cos(2t))/(4+t^2 ))dt 3) let U_n =∫_0 ^∞ ((cos(nt))/(n^2 +t^2 ))dt find lim_(n→+∞) U_n and study the convergenge of Σ U_n and Σ U_n ^2 |
| let f(x)=∫_(−∞) ^(+∞) cos(t^2 +xt +3)dt with x>0 1) find f(x) 2) calculate ∫_1 ^4 f(x)dx and ∫_1 ^(+∞) f(x)dx |
| Evaluate : 1) ((∫_0 ^( 1_ ) (1−(1−x^2 )^(100) )^(201) .xdx)/(∫_0 ^( 1) (1−(1−x^2 )^(100) )^(202) .xdx)) = ? 2) ((∫_0 ^( 1) (1−x^(200) )^(201) dx)/(∫_0 ^( 1) (1−x^(200) )^(202) dx)) = ? |
| let u_n =∫_(−∞) ^∞ ((sin(nx^2 ))/(x^2 +x +n)) dx 1) calculate u_n 2) find lim_(n→+∞) u_n 3) study the serie Σ u_n |
| find the value of ∫_0 ^∞ (((1+x)^(−(1/4)) −(1+x)^(−(3/4)) )/x) dx |
| study the convergence of ∫_0 ^∞ (((1+x)^α −(1+x)^β )/x) dx . |
| calculate ∫_0 ^∞ ((arctan(ix))/(2+x^2 ))dx |
| ∫^1 _(−∞) (a+bi)^x dx=? |
| ∫_(−1) ^0 ∣x sin (πx)∣ dx |
| ∫_0 ^1 e^(−x^2 ) dx correct to 3 decimal place. |
| ∫e^(−x^2 ) dx as an infinite series.Hence investigate its converge. |
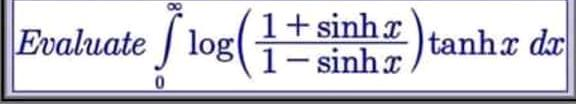
|
| find f(x) =∫_0 ^1 arctan(t^2 +xt +1)dt . |
| calculate ∫_(π/3) ^(π/2) (dx/(x+sinx)) |
| find ∫_(π/3) ^(π/2) (x/(cosx))dx |
| find I =∫ arctan(1−x)dx and J =∫ actan(1+x) dx |
| calculate ∫_0 ^1 arctan(x^2 −x)dx |

|
| ∫_0 ^( π) ((xtan x)/(sec x+tan x))dx = (is it (π^2 /2)−π)? |
| Integrate..∫(√(1+(√(1+(√x))))) dx |
Pg 235 Pg 236 Pg 237 Pg 238 Pg 239 Pg 240 Pg 241 Pg 242 Pg 243 Pg 244 |