
Question and Answers Forum
IntegrationQuestion and Answers: Page 241

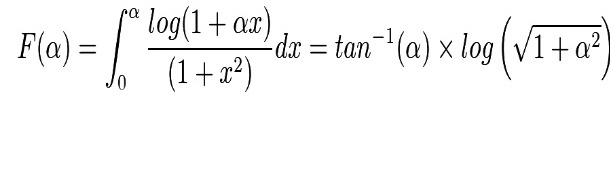
Pg 236 Pg 237 Pg 238 Pg 239 Pg 240 Pg 241 Pg 242 Pg 243 Pg 244 Pg 245
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 241 |
| For all n ∈ N f_n (x)= { ((((nx)/(2n−1)), x ∈ [0, ((2n−1)/n)])),((1 , x ∈[((2n−1)/n), 2])) :} then for n→∞ ∫_1 ^2 f_n (x) dx convergences to.. |
| let F(α)=∫_α ^(1+α^2 ) ((sin(αx))/(1+αx^2 ))dx 1) calculate (dF/dα)(α) 2) calculate lim_(α→0) F(α) |
| let u_n = ∫_(π/(n+1)) ^(π/n) (√(tan(x)))dx with n≥3 1) calculate U_n interms of n and calculate lim_(n→+∞ ) U_n 2) find nature of the serie Σ_(n≥3) U_n |

|
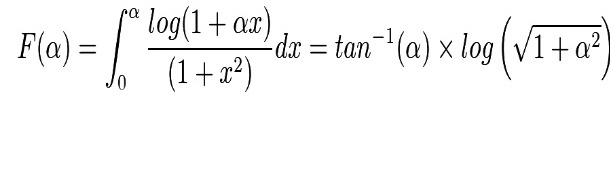
|
| How can solve ∫(√)tan(x)dx ? |
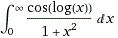
|
| calculate ∫_0 ^∞ ((ln(x))/(x^2 +x+1))dx . |
| prove that ∫_(−∞ ) ^∞ f(x)dx=1 such that f(x)=(1/((√n) β((n/2),(1/2))))(1+(x^2 /n))^(−(1/2)(1+n)) and β((n/2),(1/2))=∫_0 ^∞ (x^((n/2)−1) /((1+x)^(3/2) ))dx |
| ∫_1 ^( 2) (√(sin (3x−x^2 −2)))dx + (1/2)∫_3 ^1 (√(sin(((4t−t^2 −3)/4))))dt =? |
| ∫ 3x(√( 3x^3 + 7)) dx = . . . . |
| calculatef(a)= ∫ (1+(a/x^2 ))arctan((a/x))dx 2) calculate ∫_1 ^(+∞) (1+(2/x^2 ))arctan((2/x))dx . |
| fint f(t)=∫_0 ^1 ((ln(1+tx^2 ))/x^2 )dx . |
| find L( e^(−x) ln(1+x^2 )) with L mean laplace transform |
| calculate ∫_0 ^(+∞) (dx/((x+1)(x+2)....(x+n))) |
| let ϕ(a) =∫_1 ^(√3) arctan((a/x))dx 1) calculate ϕ(a) interms of a 2) calculate ϕ^′ (a) at form of integral. 3) determine ϕ^((n)) (a) at form of integral. 4) find the value of ∫_1 ^(√3) arctan((2/x))dx . |
| let f(x) =∫_x^2 ^(1+x) (dt/(1+t+t^2 )) 1) calculate f(x) interms of x 2) calculate lim_(x→0) f(x) and lim_(x→+∞) f(x) |
| 1) let f(x) =∫_0 ^(2π) ((cost)/(3 +sin(xt)))dt find a explicit form of f(x) 2) calculate g(x) =∫_0 ^(2π) ((tcos(xt)cost)/((3 +sin(xt))^2 ))dt 3) calculate ∫_0 ^(2π) ((cost)/(3+sint)) and ∫_0 ^(2π) ((t cos^2 t)/((3+sint)^2 ))dt |
| 1) calculate f(x)=∫_0 ^(π/4) ln(1+xtanθ)dθ 2) find the values of integrals ∫_0 ^(π/4) ln(1+tanθ) and ∫_0 ^(π/4) ln(1+2tanθ)dθ . 1) we have f^′ (x)=∫_0 ^(π/4) ((tanθ)/(1+xtanθ)) dθ =∫_0 ^(π/4) (((sinθ)/(cosθ))/(1+x((sinθ)/(cosθ))))dθ =∫_0 ^(π/4) ((sinθ)/(cosθ +xsinθ)) dθ =_(tan((θ/2))=t) ∫_0 ^((√2)−1) (((2t)/(1+t^2 ))/(((1−t^2 )/(1+t^2 )) +((2xt)/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫_0 ^((√2)−1) ((4t)/((1+t^2 )(1−t^2 +2xt)))dt =−∫_0 ^((√2)−1) ((4t)/((t^2 +1)(t^2 −2xt −1)))dt let decompose F(t) = ((4t)/((t^2 +1)(t^2 −2xt −1))) roots of t^2 −2xt −1 Δ^′ =x^2 +1 ⇒t_1 =x+(√(x^2 +1)) and t_2 =x−(√(x^2 +1)) F(t)=(a/(t−t_1 )) +(b/(t−t_2 )) +((ct +d)/(t^2 +1)) a =lim_(t→t_1 ) (t−t_1 )F(t)=((4t_1 )/((t_1 ^2 +1)(t_1 −t_2 ))) =α b =lim_(t→t_2 ) (t−t_2 )F(t) =((4t_2 )/((t_2 ^2 +1)(t_2 −t_1 ))) =β ⇒F(t)=(α/(t−t_1 )) +(β/(t−t_2 )) +((ct +d)/(t^2 +1)) F(0) =0=−(α/t_1 ) −(β/t_2 ) +d ⇒d =(α/t_1 ) +(β/t_2 ) F(1)=(2/(−2x)) =−(1/x)=(α/(1−t_1 )) +(β/(1−t_2 )) +((c+d)/2) ⇒(1/x) =(α/(t_1 −1)) +(β/(t_2 −1)) −(c/2) −(d/2) ⇒(c/2) =(α/(t_1 −1)) +(β/(t_2 −1)) −(d/2) −(1/x) ⇒c =((2α)/(t_1 −1)) +((2β)/(t_2 −1)) −d−(2/x) ∫ F(t)dt =αln∣t−t_1 ∣ +βln∣t−t_2 ∣ +(c/2)ln(t^2 +1) +d arctan(t) ⇒ ∫_0 ^((√2)−1) F(t)dt =[αln∣t−t_1 ∣+βln∣t−t_2 ∣ +(c/2)ln(t^2 +1)]_0 ^((√2)−1) =αln∣(√2)−1−t_1 ∣ +βln∣(√2)−1−t_2 ∣ +(c/2)ln(4−2(√2)) =αln∣(√2)−1−x−(√(1+x^2 )))+βln∣(√2)−1−x+(√(1+x^2 ))) +((ln(4−2(√2)))/2)c =f^′ (x) ⇒ f(x)=∫ αln∣(√2)−1−x−(√(1+x^2 ))∣)dx+β∫ ln∣(√2)−1+(√(1+x^2 ))∣dx +((cx)/2)ln(4−2(√2)) +C ....be continued... |
| ∫_0 ^3 ∫_1 ^2 (x^3 +y^2 )dxdy |
| calculate lim_(ξ→0) ∫_1 ^(1+ξ) ((arctan(ξt))/t) dt . |
| calculate lim_(n→+∞) ∫_0 ^n (e^(nx) /(1+nx^2 )) dx . |
|
| let U_n =∫_(1/n) ^1 (√(x^2 +(3/n)))dx .calculate lim_(n→+∞) U_n |
| ∫(dα/(1−sin^3 α))=? ∫(dβ/(1−cos^3 β))=? ∫(dγ/(1−tan^3 γ))=? |
| question 54995 reposted ∫((x^3 +x^2 ))^(1/3) dx=? |
Pg 236 Pg 237 Pg 238 Pg 239 Pg 240 Pg 241 Pg 242 Pg 243 Pg 244 Pg 245 |