
Question and Answers Forum
IntegrationQuestion and Answers: Page 244


Pg 239 Pg 240 Pg 241 Pg 242 Pg 243 Pg 244 Pg 245 Pg 246 Pg 247 Pg 248
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 244 |
| the absolute value ∫_(10) ^(19) ((cos x)/(1+x^8 )) dx is... |
| Evaluate : 1) ∫_0 ^( 1) (dx/((√(1+x))+(√(1−x))+2)) 2) ∫_0 ^( 2) ((ln(1+2x))/(1+x^2 )) 3) ∫_0 ^( π) (x/(√(1+sin^3 x)))((3πcosx+4sinx)sin^2 x+4)dx 4) ∫_0 ^( π) ((x^2 cos^2 x−xsinx−cosx−1)/((1+xsinx)^2 )) dx. |

|
| Evaluate : 1) ∫_(−1) ^( 1) cot^(−1) ((1/(√(1−x^2 )))).(cot^(−1) (x/(√(1−(x^2 )^(∣x∣) ))))dx 2) ∫_0 ^( (π/2)) ((sin^2 (10)θ)/(sin^2 θ)) dθ 3) ∫_0 ^( (π/4)) ((ln(cotx))/(((sinx)^(2009) +(cosx)^(2009) )^2 )).(sin2x)^(2008) dx 4) ∫_0 ^( 2) ((4x+10)/((x^2 +5x+6)^2 )) dx. |
| calculate f(a) =∫ (dx/((√(1+ax))−(√(1−ax)))) with a>0 . 2) calculate U_n =∫_(−(1/(na))) ^(1/(na)) (dx/((√(1+ax))−(√(1−ax)))) with n from N and n>1 find lim_(n→+∞) U_n and study the convergence of Σ U_n |
| 1)calculate A_t =∫_0 ^∞ e^(−xt) sinxdx with x>0 2) by using Fubuni theorem find the value of ∫_0 ^∞ ((sinx)/x)dx . |
| let f(x) =xsinx ,2π periodic even developp f at Fourier serie . |
| give∫_0 ^1 e^(−x) ln(1−x)dx at form of serie |
| calculate ∫_(1/3) ^(1/2) Γ(x)Γ(1−x)dx with Γ(x) =∫_0 ^∞ t^(x−1) e^(−t) dt with x>0 . |
| find the value of ∫_0 ^1 ln(x)ln(1−x^2 )dx |
| let f(x) = x∣x∣ , 2π periodic odd developp f at fourier serie . |
| ∫x!dx |
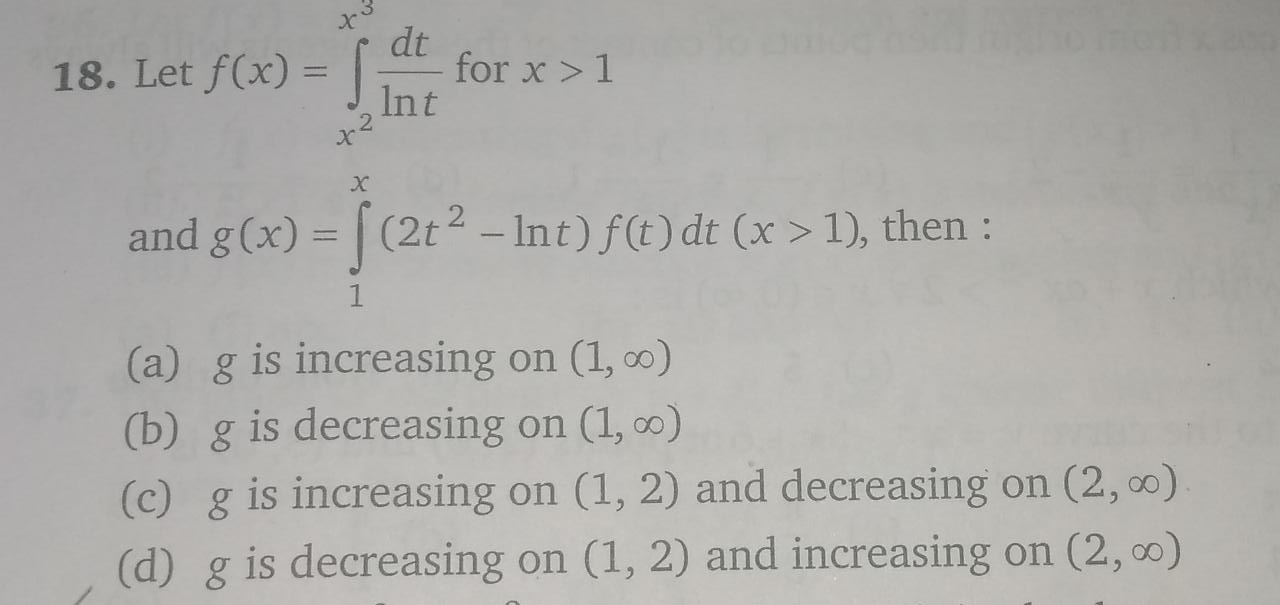
|
| let f(x)=∫_0 ^∞ ((tsin(tx))/(1+t^4 ))dt with x>0 1) find a explicit form of f(x) 2) find the value of ∫_0 ^∞ ((tsin(2t))/(1+t^4 ))dt. |
| calculate ∫_0 ^∞ (t^2 /(e^t −1))dt interms of ξ(3) |
| calculate ∫_0 ^1 (t^2 /(1+t^3 ))dt |
| find ∫_(−∞) ^(+∞) e^(−x^2 ) (√(1+2x^2 ))dx |
| 1) study the function f(x)=ln(x+1−(√x)) 2) determine f^(−1) (x) 3) cslculate ∫ f(x)dx snd ∫ f^(−1) (x)dx 4) dtermine ∫ f^(−1) (x^2 +f(x))dx |
| calculate ∫_0 ^∞ ((e^(−x^2 ) −e^(−x) )/x) dx . |
| calculate A_m =∫_0 ^∞ ((sin(mx))/(e^(2πx) −1)) dx with m>0 |
| 1) calculate A_n =∫_0 ^∞ (x^(n−1) /(e^x +1)) dx with n integr natural (n≥2) 2) find the value of ∫_0 ^∞ (x/(e^x +1))dx |

|
| let f(a)=∫_0 ^1 (dt/((√(x+a)) +3)) 1) calculate f(a) 2) find also ∫_0 ^1 (dt/((√(x+a))((√(x+a)) +3)^2 )) 3) find the values of integrals ∫_0 ^1 (dt/((√(x+1))+3)) and ∫_0 ^1 (dt/((√(x+1))((√(x+1))+3)^2 )) |
| let f(x)=∫_0 ^x t(√(2t−1))dt calculate ∣sup_(1≤x≤2) f(x) −inf_(1≤x≤2) f(x)∣ |
| calculate ∫_0 ^1 ((5^(2x+1) −2^(2x−1) )/(10^x )) dx |
| 1)find U_n = ∫_0 ^(π/4) tan^n tdt with n integr . 2) find lim_(n→+∞) U_n 3) calculate Σ_(n=0) ^∞ U_n |
Pg 239 Pg 240 Pg 241 Pg 242 Pg 243 Pg 244 Pg 245 Pg 246 Pg 247 Pg 248 |