
Question and Answers Forum
IntegrationQuestion and Answers: Page 249



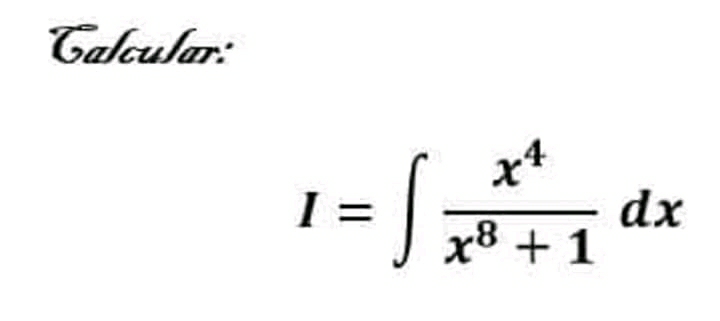

Pg 244 Pg 245 Pg 246 Pg 247 Pg 248 Pg 249 Pg 250 Pg 251 Pg 252 Pg 253
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 249 |
| find ∫ (dx/((1−x^2 )(1−x^3 ))) 2) calculate ∫_2 ^(√5) (dx/((1−x^2 )(1−x^3 ))) |

|
| find f(a) =∫_a ^(+∞) (dx/((1+x^2 )(√(x^2 −a^2 )))) with a>0 |
| Let f(x)= ∫_2 ^( x) (dt/(1+t^6 )). Prove that : (1/(730))<f(3)<(1/(65)). |
| Find the function whose first derivative is 8−(5/(x^2 )^(1/3) ) the initial conditions f(8)=−20 |

|
|
| For a < x < b, find ∫_a ^b (√(x−a)) . (√(b−x)) dx |
| find f(x) =∫_0 ^(+∞) ((t arctan(xt))/(1+t^4 )) dt |
| calculate ∫_0 ^(+∞) (dx/((x^2 −i)^2 )) |
| find ∫_0 ^1 cos(n arcosx)dx with n integr natural. |
| 1) calculate ∫_0 ^1 ln(1+ix)dx and ∫_0 ^1 ln(1−ix)dx 2) find the value of ∫_0 ^1 ln(1+x^2 )dx . |

|
| find f(α) =∫_0 ^1 ((arctan(αx))/(1+α^2 x^2 ))dx 2) calculate ∫_0 ^1 ((arctan(2x))/(1+4x^2 )) dx and ∫_0 ^1 ((arctan(3x))/(1+9x^2 )) dx . |
| calculate ∫∫_D (√(x^4 −y^4 ))dxdy with D =[0,1]×[0,1] |
| calculate ∫_0 ^1 e^(−x) ln(1+x)dx |
| find ∫_0 ^(π/2) sinx ln(1+x) dx |
| find f(x)=∫_0 ^(π/4) ln(cost+xsint)dt |
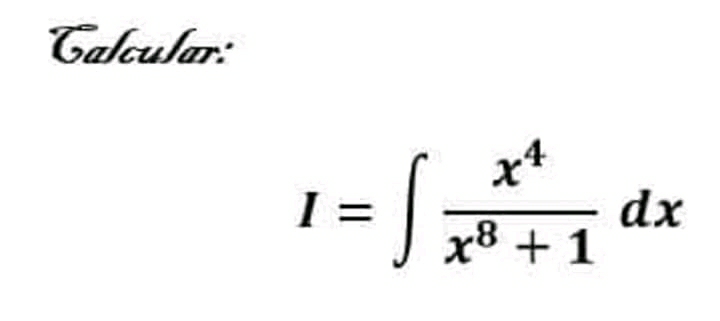
|
| If F(t)= ∫_0 ^( t) e^(t−y) .ydy. Prove that F(t)= e^t −(1+t). |

|
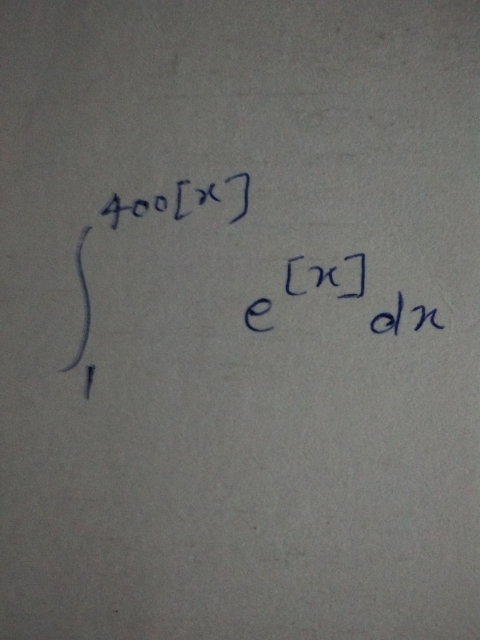
|
| ∫(dx/(√((a+1)cos 2x +4cos x −a+3)))=? |
| ∫(x^2 /(x^4 +1))dx |
| The integral ∫_0 ^(1/2) ((ln (1+2x))/(1+4x^2 ))dx = ? a) (π/4)ln2 b)(π/8)ln2 c)(π/(16))ln2 d)(π/(32))ln2 |
| ((sin^6 x−cos^6 x)/(sin^2 xcos^2 x)).intregrate |
Pg 244 Pg 245 Pg 246 Pg 247 Pg 248 Pg 249 Pg 250 Pg 251 Pg 252 Pg 253 |