
Question and Answers Forum
IntegrationQuestion and Answers: Page 250
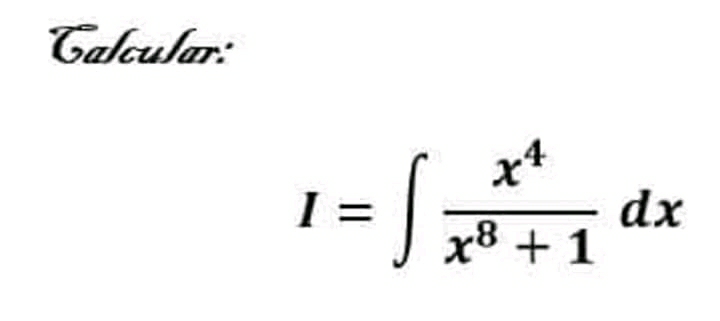

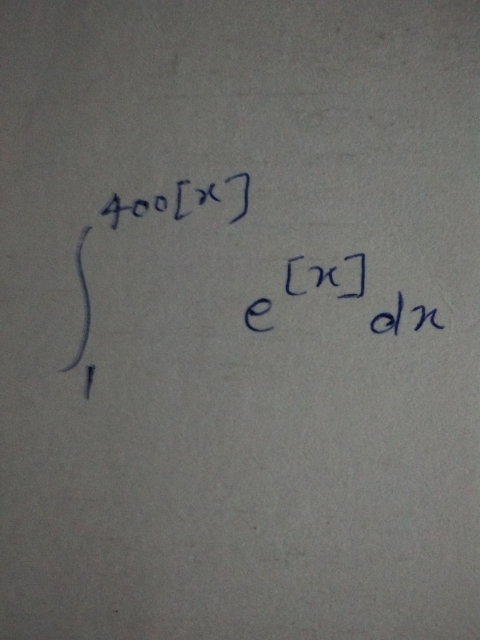


Pg 245 Pg 246 Pg 247 Pg 248 Pg 249 Pg 250 Pg 251 Pg 252 Pg 253 Pg 254
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 250 |
| find f(x)=∫_0 ^(π/4) ln(cost+xsint)dt |
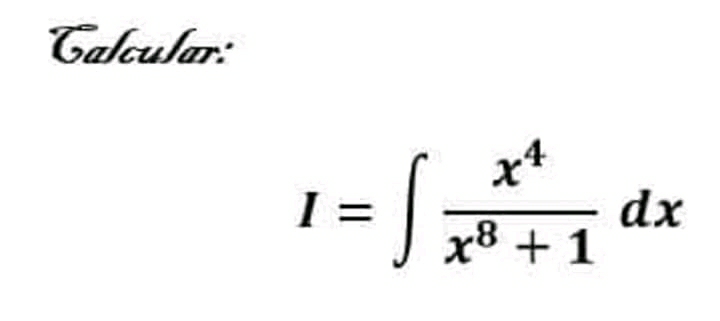
|
| If F(t)= ∫_0 ^( t) e^(t−y) .ydy. Prove that F(t)= e^t −(1+t). |

|
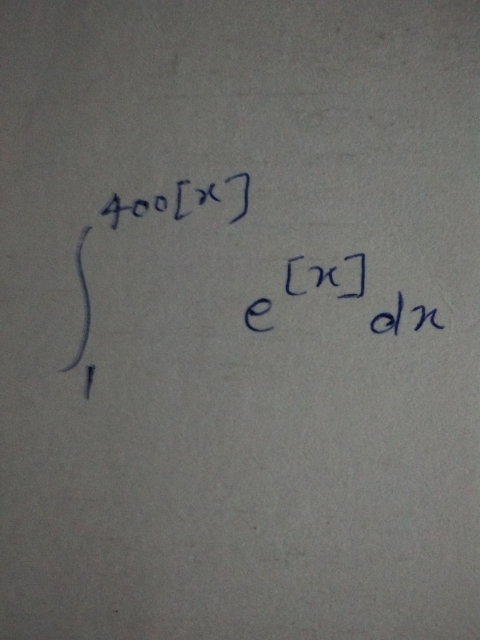
|
| ∫(dx/(√((a+1)cos 2x +4cos x −a+3)))=? |
| ∫(x^2 /(x^4 +1))dx |
| The integral ∫_0 ^(1/2) ((ln (1+2x))/(1+4x^2 ))dx = ? a) (π/4)ln2 b)(π/8)ln2 c)(π/(16))ln2 d)(π/(32))ln2 |
| ((sin^6 x−cos^6 x)/(sin^2 xcos^2 x)).intregrate |
| sin^6 x−cos^6 x/sin^2 xcos^2 x |
| let f(x) =∫_0 ^(π/4) ln(1−x^2 cosθ)dθ with ∣x∣<1 1) find a explicit form of f(x) 2) calculate ∫_0 ^(π/4) ln(1−(1/4)cosθ)dθ . |
| Calculate : ∫(( sin^2 x cos^2 x)/((sin^3 x+cos^3 x)^2 )) dx |

|
| ∫((sin^8 x−cos^8 x)/(1−2sin^2 x.cos^2 x)) = ? a) ((−1)/2)sin 2x b)(1/2)sin 2x c)None. |
| Please integrate ∫(((e^(cos x) sin x)/(1−x^2 )))dx |
| calculateA_n =(1/(2i)) ∫_0 ^1 {(1+ix)^n −(1−ix)^n }dx |
| calculate ∫∫_D (x^2 −y^2 )(√(x^2 +y^2 ))dxdy with D ={(x,y)∈R^2 / −1≤x≤1 and 0≤y≤2 } |
| calculate ∫∫_C ∣x+y∣dxdy with C=[−1,1]×[−1,1] |
| 1) calculate A_n =∫_0 ^∞ e^(−n[x]) sin(x)dx with n integr and n≥1 2) find nature of Σ_(n=1) ^∞ A_n |
| 1)find f(x) =∫_0 ^(π/4) ((sint)/(2+x cos(2t)))dt 2) find g(x) =∫_0 ^(π/4) ((sint sin(2t)/((2+x cos(2t))^2 ))dx 3) find the value of ∫_0 ^(π/4) ((sint)/(2+3 cos(2t)))dt and ∫_0 ^(π/4) ((sin(t)sin(2t))/((2+3cos(2t))^2 ))dt |
| evaluate ∫x^(3 ) J_3 (x)dx |

|
| a) ∫ (dx/(√(1−tgx))) b)∫ (dx/((1−tgx))^(1/3) ) c)∫ (dx/(√(1−(√(1−x))))) |
| let α>0 calculate ∫_(−∞) ^(+∞) (1+αi)^(−x^2 ) dx . |
| find ∫_0 ^1 ((ln(x))/(1+x))dx . |
| find ∫_0 ^1 (e^x /(1+x))dx . |
Pg 245 Pg 246 Pg 247 Pg 248 Pg 249 Pg 250 Pg 251 Pg 252 Pg 253 Pg 254 |