
Question and Answers Forum
IntegrationQuestion and Answers: Page 254
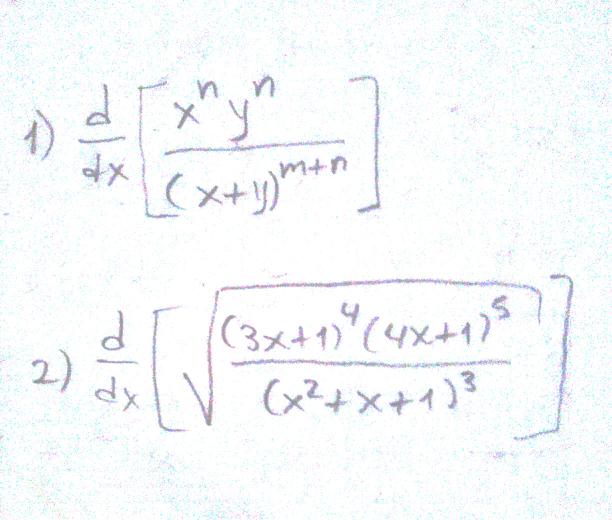




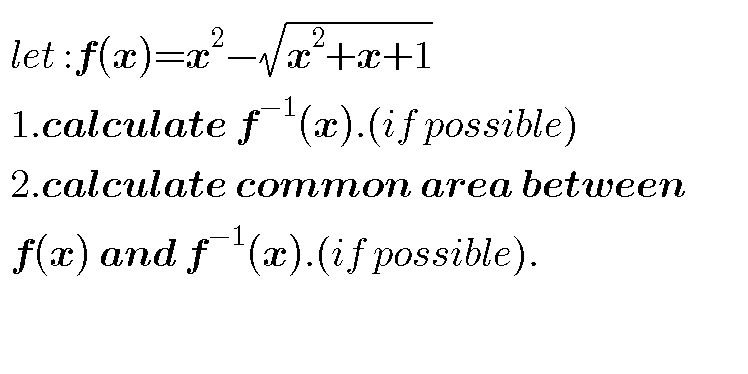
Pg 249 Pg 250 Pg 251 Pg 252 Pg 253 Pg 254 Pg 255 Pg 256 Pg 257 Pg 258
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 254 |
| let f(x) =∫_(1/2) ^1 (dt/(2+ch(xt))) 1) find a explicit form of f(x) 2) calculate g(x)=∫_(1/2) ^1 ((tsh(xt))/((2+ch(xt))^2 ))dt 3) find the value of ∫_(1/2) ^1 (dt/(2+ch(3t))) and ∫_(1/2) ^1 ((tsh(2t))/((2+ch(2t))^2 ))dt 4) let u_n =∫_(1/2) ^1 (dt/(2+ch(nt))) study the convergence of Σu_n and Σ(u_n /n) . |
| calculate A_λ =∫_0 ^∞ ((cos(λsinx)−sin(λcosx))/(x^2 +λ^2 ))dx λ from R. |
| q.....∫(dx/(sin x cos x+2cos^2 x)), please solve |
|
| find ∫ ((sin(πx))/(3 +cos(2πx)))dx |
| find lim_(x→0) ∫_(x+1) ^(2x+1) ((tarctan(t^2 +1))/(1+(1+t^2 )^2 ))dt |
| calculate lim_(x→0) ∫_x ^x^2 ((ln(1+t))/(sin(t)))dt |
| calculate ∫ ((arctan(x))/(√(1+x^2 )))dx |
| calculate ∫_0 ^∞ ((sin(2cos(x^2 +1)))/(1+x^2 ))dx |
| calculate ∫_0 ^∞ ((sin(cosx))/(x^2 +3))dx |
| calculate ∫_0 ^∞ ((cos(sin(x^2 )))/(1+2x^2 ))dx |

|
| solve this ∫(2 sinx+cosx)/(2+3sinx+sin^(2x) ) dx |

|
| let y>0 give ∫_0 ^∞ (x^y /(e^x −1))dx at form of series. |
| calculate A =∫_0 ^1 (1+x^2 )(√(1−x^2 ))dx −∫_0 ^1 (1−x^2 )(√(1+x^2 ))dx |
| let W(x) =∫_(−∞) ^(+∞) ((arctan(xt^2 ))/(2+t^2 ))dt 1) find a explicit form of f(x) 2) find the value of ∫_(−∞) ^(+∞) (t^2 /((2+t^2 )(1+x^2 t^4 )))dt . |
| calculate ∫_(−∞) ^(+∞) (((x^2 −3)sin(2x^2 ))/((x^2 +1)^3 ))dx |

|
| let f(α) =∫_(−∞) ^(+∞) ((cos(αx^3 ))/(x^2 +8)) dx 1)calculate f(α) 2) calculate ∫_(−∞) ^(+∞) ((cos(2x^3 ))/(x^2 +8))dx . |
| find the value of ∫_(−∞) ^(+∞) ((2x+1)/((x^2 +i)(x^2 +4)))dx (i^2 =−1) |
| let f(α)=∫_(−∞) ^(+∞) ((xsin(αx))/((1+x^2 )^2 ))dx calculate f(α) and f^′ (α).(α from R) . |

|
| calculate I=∫_0 ^1 (√(1+2(√(x−x^2 ))))dx and J =∫_0 ^1 (√(1−2(√(x−x^2 ))))dx |
| A particle moves in a linear scare such that acceleration after t seconds is a ms^(−2) where a= 2t^2 + t.If its initial velocity was 3ms^(−1) find an expression for S,the distance in meters traveled from start t seconds. |
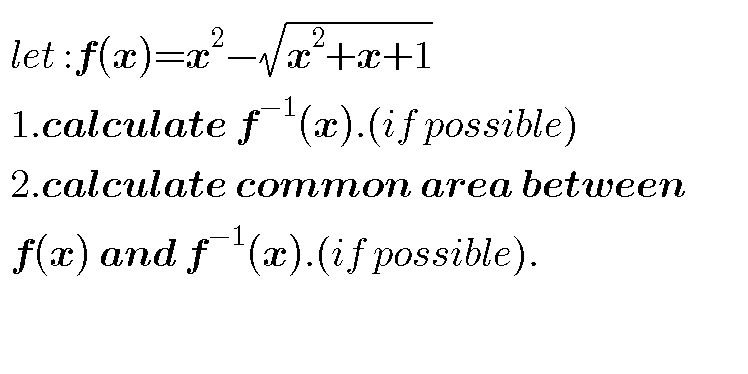
|
Pg 249 Pg 250 Pg 251 Pg 252 Pg 253 Pg 254 Pg 255 Pg 256 Pg 257 Pg 258 |