Question and Answers Forum

IntegrationQuestion and Answers: Page 26

Question Number 190623 Answers: 2 Comments: 0

calculate : Σ_(n=1) ^∞ (( (−1)^( n−1) )/n) cos ((( nπ)/3) ) =?

$calculate :$ $\underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n - 1}}{n} \cos (\frac{n π}{3}) = ?$

Question Number 190622 Answers: 1 Comments: 0

prove : ∫_(−∞) ^( ∞) ((( x)/( ⋮ )^2 dx= Σ_(k=1) ^∞ (1/( k^2 )) ⋖))

$p r o v e :$ $\int_{- \infty}^{\infty} (\frac{x}{{\underset{―}{⋮})}^{2} d x = \underset{k = 1}{\sum^{\infty}} \frac{1}{k^{2}} ⋖}$

Question Number 190552 Answers: 1 Comments: 1

∫_(1/2) ^2 ln(((ln(x+(1/x)))/(ln(x^2 −x+((17)/6)))))dx=?

$\int_{\frac{1}{2}}^{2} l n (\frac{l n (x + \frac{1}{x})}{l n (x^{2} - x + \frac{17}{6})}) d x = ?$

Question Number 190533 Answers: 1 Comments: 0

Question Number 190487 Answers: 1 Comments: 0

Question Number 190419 Answers: 1 Comments: 0

∫_(−1) ^1 ∫_(−(√(1−y^2 ))) ^(√(1−y^2 )) ln (x^2 +y^2 +1)dx dy =?

$\underset{- 1}{\int^{1}} \underset{- \sqrt{1 - y^{2}}}{\int^{\sqrt{1 - y^{2}}}} \ln (x^{2} + y^{2} + 1) d x d y = ?$

Question Number 190385 Answers: 1 Comments: 0

Question Number 190371 Answers: 1 Comments: 0

Question Number 190360 Answers: 3 Comments: 0

if x+ (1/x) = ϕ ( Golden ratio) ⇒ x^( 2000) + (1/x^( 2000) )=?

$i f x + \frac{1}{x} = φ (G o l d e n r a t i o)$ $\Rightarrow x^{2000} + \frac{1}{x^{2000}} = ?$

Question Number 190318 Answers: 2 Comments: 0

Question Number 190172 Answers: 1 Comments: 0

Integrate ∫_0 ^1 Sin^2 (2Πx)dx

$I n t e g r a t e$ $\int_{0}^{1} {S i n}^{2} (2 Π x) d x$

Question Number 190168 Answers: 0 Comments: 2

1)∫^∞ _0 ((sin x)/(x^p +sin x))dx ,p>0 2)∫^∞ _π ((xcos x)/(x^p +x^q ))dx,p>0and q>0 3)∫^∞ _0 ((sin x^p )/( x^q ))dx, p>0,q>0 4)∫^2 _0 (dx/(∣ln x∣^p )) ,p>0 5)∫^1 _0 ((cos(1/(1−x)))/( ((1−x^2 ))^(1/n) ))dx 6)∫^∞ _0 (dx/(x^p ((sin^2 x))^(1/3) ))

$1) {\int_{0}}^{\infty} \frac{s i n x}{x^{p} + s i n x} d x, p > 0$ $2) {\int_{π}}^{\infty} \frac{x c o s x}{x^{p} + x^{q}} d x, p > 0 a n d q > 0$ $3) {\int_{0}}^{\infty} \frac{s i n x^{p}}{x^{q}} d x, p > 0, q > 0$ $4) {\int_{0}}^{2} \frac{d x}{∣ l n x ∣^{p}}, p > 0$ $5) {\int_{0}}^{1} \frac{c o s \frac{1}{1 - x}}{\sqrt[n]{1 - x^{2}}} d x$ $6) {\int_{0}}^{\infty} \frac{d x}{x^{p} \sqrt[3]{{s i n}^{2} x}}$

Question Number 190009 Answers: 0 Comments: 2

Question Number 189949 Answers: 1 Comments: 0

Question Number 189890 Answers: 0 Comments: 0

Question Number 189825 Answers: 2 Comments: 0

∫^b _a (√((x−a)(b−x)))=¿

${\int_{a}}^{b} \sqrt{(x - a) (b - x)} = ¿$

Question Number 189756 Answers: 0 Comments: 0

Question Number 189752 Answers: 1 Comments: 0

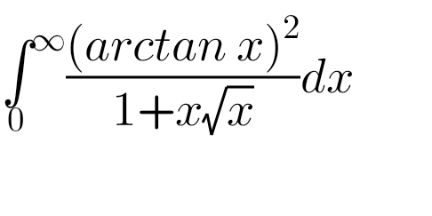
∫^∞ _0 x^2 .e^(−x^2 ) dx=¿

${\int_{0}}^{\infty} x^{2} . e^{- x^{2}} d x = ¿$

Question Number 189639 Answers: 1 Comments: 1

(((20)),(( 0)) ) (((10)),(( 1)) ) + (((20)),(( 1)) ) (((10)),(( 2)) ) +...+ ((( 20)),(( 9)) ) ((( 10)),(( 10)) ) =?

$(\begin{matrix} 20 \\ 0 \end{matrix}) (\begin{matrix} 10 \\ 1 \end{matrix}) + (\begin{matrix} 20 \\ 1 \end{matrix}) (\begin{matrix} 10 \\ 2 \end{matrix}) + . . . + (\begin{matrix} 20 \\ 9 \end{matrix}) (\begin{matrix} 10 \\ 10 \end{matrix}) = ?$

Question Number 189549 Answers: 1 Comments: 0

∫_0 ^( 1) ∫_0 ^( 1) ((dxdy)/((1+xy )^( 4) ))=?

$\int_{0}^{1} \int_{0}^{1} \frac{d x d y}{{(1 + x y)}^{4}} = ?$

Question Number 189496 Answers: 2 Comments: 0

∫ xe^(x^2 /2) dx

$\int {xe}^{\frac{x^{2}}{2}} dx$

Question Number 189489 Answers: 1 Comments: 1

Ω= ∫_0 ^( ∞) e^( −x) cos(x)ln(x)dx=? −−− f (a )= ∫_0 ^( ∞) e^( −x) cos(x)x^( a) dx = Re ∫_0 ^( ∞) e^( −x) .e^( −ix) .x^( a) dx = Re ∫_0 ^( ∞) e^( −x (1+i)) .x^( a) dx = Re(L { x^( a) }∣_( s= i+1) ) = Re( ((Γ (1+a))/s^( a+1) ) ∣_( 1+i) = ((Γ (1+a))/((1+i)^( a+1) )) ) Re (Γ(1+a).2^( ((1+a)/2)) . e^( −((iπ)/4) (1+a)) ) Ω= f ′(0)=.......

$Ω = \int_{0}^{\infty} e^{- x} c o s (x) l n (x) d x = ?$ $- - -$ $f (a) = \int_{0}^{\infty} e^{- x} c o s (x) x^{a} d x$ $= R e \int_{0}^{\infty} e^{- x} . e^{- i x} . x^{a} d x$ $= R e \int_{0}^{\infty} e^{- x (1 + i)} . x^{a} d x$ $= R e (L {x^{a}} ∣_{s = i + 1})$ $= R e (\frac{Γ (1 + a)}{s^{a + 1}} ∣_{1 + i} = \frac{Γ (1 + a)}{{(1 + i)}^{a + 1}})$ $R e (Γ (1 + a) . 2^{\frac{1 + a}{2}} . e^{- \frac{i π}{4} (1 + a)})$ $Ω = f^{'} (0) = . . . . . . .$

Question Number 189418 Answers: 1 Comments: 0

Know: f(x)=3x+2+∫^1 _0 xf(x)dx Eluavte: ∫^2 _0 f(x)dx=¿

$K n o w : f (x) = 3 x + 2 + {\int_{0}}^{1} x f (x) d x$ $E l u a v t e : {\int_{0}}^{2} f (x) d x = ¿$

Question Number 189390 Answers: 0 Comments: 0

Question Number 189345 Answers: 1 Comments: 0

solve ∫t^(−6) (t^2 +3)^2 dt

$s o l v e$ $\int t^{- 6} {(t^{2} + 3)}^{2} d t$

Question Number 189325 Answers: 2 Comments: 0

prove Ω= ∫_0 ^(π/2) (( cos(x)+cos(5x))/(1+ 2sin(x))) =^( ?) (3/2)

$p r o v e$ $Ω = \int_{0}^{\frac{π}{2}} \frac{c o s (x) + c o s (5 x)}{1 + 2 s i n (x)} \overset{?}{=} \frac{3}{2}$

Pg 21 Pg 22 Pg 23 Pg 24 Pg 25 Pg 26 Pg 27 Pg 28 Pg 29 Pg 30

Contact: info@tinkutara.com