Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 29

Question Number 186736 Answers: 1 Comments: 0

Question Number 186735 Answers: 1 Comments: 0

Question Number 186726 Answers: 2 Comments: 0

Question Number 186637 Answers: 2 Comments: 0

Question Number 186531 Answers: 0 Comments: 0

Q.use the parseval relation of hankel transfrom to evaluate the Integral ∫_0 ^∞ ((J_(𝛄+1) (ar)J_(𝛄+1) (br))/r) , for 𝛄>−(1/2) , 0<a<b where J_n (x) are bessel funtions.

$Q . u s e t h e p a r s e v a l r e l a t i o n o f h a n k e l t r a n s f r o m t o e v a l u a t e t h e I n t e g r a l$ ${\int^{\infty}}_{0} \frac{J_{γ + 1} (a r) J_{γ + 1} (b r)}{r}, f o r γ > - \frac{1}{2}, 0 < a < b$ $w h e r e J_{n} (x) a r e b e s s e l f u n t i o n s .$

Question Number 186527 Answers: 2 Comments: 0

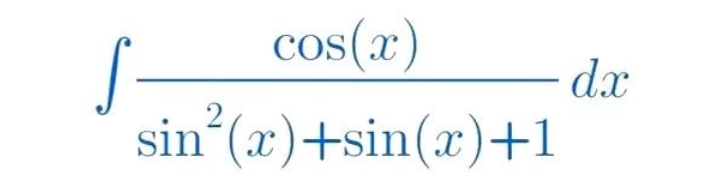
Question Number 186476 Answers: 0 Comments: 0

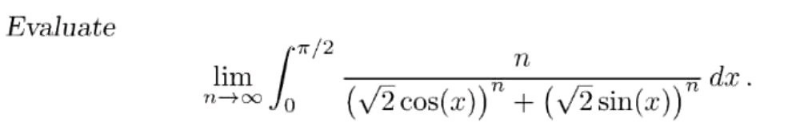
Question Number 186347 Answers: 1 Comments: 1

∫_(−2) ^2 ((x^5 − 1 + 2)/(x^4 + x −2)) dx

$\underset{- 2}{\int^{2}} \frac{x^{5} - 1 + 2}{x^{4} + x - 2} d x$

Question Number 186346 Answers: 0 Comments: 0

if S_a =cos(a)+sin(x+a) then ∫(S_1 /S_2 )−((x+S_1 )/(x−S_3 ))=?

$i f S_{a} = \cos (a) + \sin (x + a)$ $t h e n \int \frac{S_{1}}{S_{2}} - \frac{x + S_{1}}{x - S_{3}} = ?$

Question Number 186321 Answers: 3 Comments: 0

Question Number 186310 Answers: 1 Comments: 0

((∫x(x^2 +5)^(1/2) dx − 3∫x(x^2 +5)^(−1/2) dx)/(∫ ((x[(x^2 +5)−3])/( (√(x^2 +5 )))) dx)) =??

$\frac{\int x {(x^{2} + 5)}^{1 / 2} d x - 3 \int x {(x^{2} + 5)}^{- 1 / 2} d x}{\int \frac{x [(x^{2} + 5) - 3]}{\sqrt{x^{2} + 5}} d x} = ? ?$

Question Number 186306 Answers: 0 Comments: 2

Evaluate ∫((ln(sin x))/(ln(tan x)+1)) dx

$Evaluate \int \frac{\ln (\sin x)}{\ln (\tan x) + 1} d x$

Question Number 186246 Answers: 1 Comments: 0

Question Number 186352 Answers: 1 Comments: 0

∫_1 ^( 2) ((tan^(−1) (x) + 2)/x^2 ) dx

$\int_{1}^{2} \frac{{t a n}^{- 1} (x) + 2}{x^{2}} d x$

Question Number 186214 Answers: 0 Comments: 12

if S_a =cos(a)+sin(x+a) then ∫(S_1 /S_2 )−((x+S_1 )/(x−S_3 ))dx=?

$i f S_{a} = \cos (a) + \sin (x + a)$ $t h e n \int \frac{S_{1}}{S_{2}} - \frac{x + S_{1}}{x - S_{3}} d x = ?$

Question Number 186198 Answers: 1 Comments: 0

∫^3 _2 ((x^2 − 1)/(1 + ^x^2 (√(2 ln(x))))) dx

${\int_{2}}^{3} \frac{x^{2} - 1}{1 +^{x^{2}} \sqrt{2 l n (x)}} d x$

Question Number 186196 Answers: 3 Comments: 2

∫_1 ^2 (((√(1 )) + cos (x))/( (√1) − cos (x))) dx

$\underset{1}{\int^{2}} \frac{\sqrt{1} + c o s (x)}{\sqrt{1} - c o s (x)} d x$

Question Number 186195 Answers: 1 Comments: 0

∫_1 ^2 ((1/2 ∙(x^2 ) )/(x (√(x^2 + 2)))) dx

$\underset{1}{\int^{2}} \frac{1 / 2 \cdot (x^{2})}{x \sqrt{x^{2} + 2}} d x$

Question Number 186194 Answers: 1 Comments: 2

∫_2 ^4 ((2x^2 − 1)/(1 + (√x^2 ) − 2)) dx

$\underset{2}{\int^{4}} \frac{2 x^{2} - 1}{1 + \sqrt{x^{2}} - 2} d x$

Question Number 186193 Answers: 2 Comments: 0

∫_0 ^1 ((sin (x))/(1 + cos(x))) dx

$\underset{0}{\int^{1}} \frac{s i n (x)}{1 + c o s (x)} d x$

Question Number 186192 Answers: 1 Comments: 0

My old problem ∫ e^(tan x) dx

$M y o l d p r o b l e m$ $\int e^{t a n x} d x$

Question Number 186190 Answers: 0 Comments: 1

My old problem.. ∫_0 ^(+∞) ((tan^(−1) (1−cos(x)))/x^2 ) dx

$M y o l d p r o b l e m . .$ $\underset{0}{\int^{+ \infty}} \frac{\tan^{- 1} (1 - c o s (x))}{x^{2}} d x$

Question Number 186181 Answers: 1 Comments: 0

∫_0 ^π (√(1+cos^2 x)) dx =?

$\underset{0}{\int^{π}} \sqrt{1 + \cos^{2} x} d x = ?$

Question Number 186171 Answers: 1 Comments: 0

[so easy] ∫ cos^2 (4x) + sin^4 (2x) dx

$[s o e a s y]$ $\int {c o s}^{2} (4 x) + {s i n}^{4} (2 x) d x$

Question Number 186170 Answers: 1 Comments: 0

∫_(−2) ^2 ((tan^(−1) ( 2 − cos (x)) )/(2 + x^2 )) dx

$\underset{- 2}{\int^{2}} \frac{{t a n}^{- 1} (2 - c o s (x))}{2 + x^{2}} d x$

Question Number 186152 Answers: 1 Comments: 0

I= ∫_2 ^𝛑 ((cos^2 (x) − 1 )/(1 + sin (x) − tan (x))) dx

$I = \underset{2}{\int^{π}} \frac{{c o s}^{2} (x) - 1}{1 + s i n (x) - t a n (x)} d x$

Pg 24 Pg 25 Pg 26 Pg 27 Pg 28 Pg 29 Pg 30 Pg 31 Pg 32 Pg 33

Contact: info@tinkutara.com