
Question and Answers Forum
IntegrationQuestion and Answers: Page 294
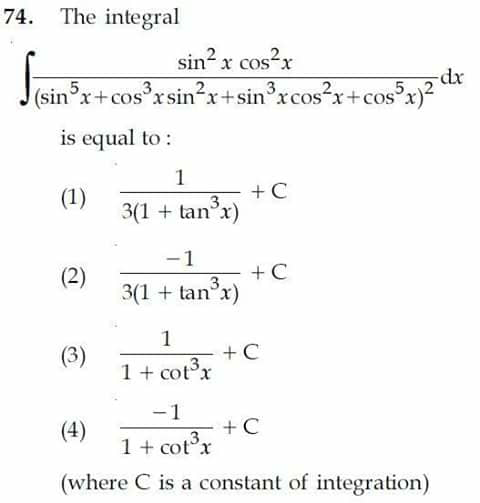
Pg 289 Pg 290 Pg 291 Pg 292 Pg 293 Pg 294 Pg 295 Pg 296 Pg 297 Pg 298
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 294 |
| let A(x)= ∫_0 ^1 ln(1+ix^2 )dx find a simple form of f(x) (x∈R) |
| let B(p,q) = ∫_0 ^1 x^(p−1) (1−x)^(q−1) dx calculate B((1/3), (1/3)) 2) calculate B((1/2) ,(2/3)) . |
| let I_n = ∫∫_([(1/n),n]^2 ) (((√(xy)) dxdy)/(2 +x^2 +y^2 )) find lim I_n when n→+∞. |
| calculate ∫∫_w x(√(x^2 +y^2 )) dxdy w ={(x,y)/ x^2 +y^2 ≤3 } |
| calculate ∫∫_(0≤x≤y≤1) ((dxdy)/((x^2 +1)(y^2 +3))) . |
| calculate ∫∫_(x^2 +2y^2 ≤1) (x^2 −y^2 )dxdy |
| let a>0 calculate ∫∫_(x^2 +y^2 ≤3) (1/(2 +x^2 +y^2 ))dxdy. |
| provethat e = Σ_(k=0) ^n (1/(k!)) +∫_0 ^1 (((1−t)^n )/(n!)) e^t dt . |
| find ∫_0 ^π ((x sinx)/(1+cos^2 x)) dx |
| calculate I(a) =∫_(1/a) ^a ((ln(x))/(1+x^2 )) dx with a>0 2) calculate ∫_0 ^(+∞) ((ln(x))/(1+x^2 )) dx . |
| let f(x)= ∫_0 ^1 (e^(−(1+t^2 )x) /(1+t^2 )) dt find a simple form of f(x) |
| calculate A(α) = ∫_0 ^1 ln(1+αix)dx 2) calculate ∫_0 ^1 ln(1+ix) dx (i^2 =−1) |
| let f(α) = ∫_(−∞) ^(+∞) ((arctan(1+αxi))/(1+x^2 ))dx find f(α) . |
| 1) calculate ∫_(−∞) ^(+∞) ((cos(αx^n ))/(x^2 +x +1)) dx with n integr natural 2) find the value of ∫_(−∞) ^∞ ((cos( α x^(2n) ))/(x^2 +x +1))dx 3) calculate ∫_(−∞) ^(+∞) ((cos(π x^3 ))/(x^2 +x +1)) dx |
| find the value of ∫_0 ^1 ((arctanx)/((1+x^2 )^2 )) dx |
| find the value of ∫_0 ^(+∞) ((arctan(x))/((1+x^2 )^2 )) dx |
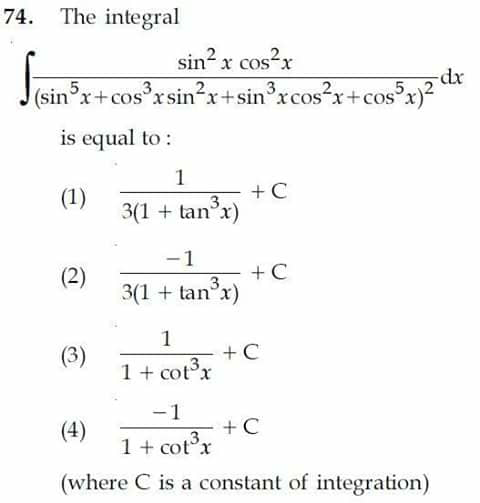
|
| let A = ∫_(−∞) ^(+∞) (dx/(x^2 −j)) with j=e^(i((2π)/3)) extract ReA and Im(A) and calculste its values. |
| calculate ∫_(−∞) ^(+∞) (dx/(x^2 +1 −i)) |
| find a eajivalent of u_n = ∫_0 ^∞ e^(−(t/n)) arcctant dt . |
| 1) find F(x)= ∫_0 ^(+∞) ((e^(−at) −e^(−bt) )/t)sin(xt)dt with a>0 ,b>0 . |
| let f(x)= ∫_0 ^(+∞) ((1−cos(xt))/t^2 ) e^(−t) dt calculate f(x) . |
| calculate I = ∫∫_D x^3 dxdy on the domain D ={(x,y)∈R^2 /1≤x≤2 , x^2 −y^2 −1≥0} |
| let I = ∫_0 ^(+∞) (((1+x)^(−(1/4)) −(1+x)^(−(3/4)) )/x)dx prove that I isconvergent and find its value . |
| let A_ = ∫_0 ^∞ e^(−x) cos[x]dx and B = ∫_0 ^∞ e^(−[x]) cosxdx calculate A−B . |
| find ∫_(−∞) ^(+∞) e^(−z t^2 ) dt with z=r e^(iθ) ∈ C . |
Pg 289 Pg 290 Pg 291 Pg 292 Pg 293 Pg 294 Pg 295 Pg 296 Pg 297 Pg 298 |