
Question and Answers Forum
IntegrationQuestion and Answers: Page 298
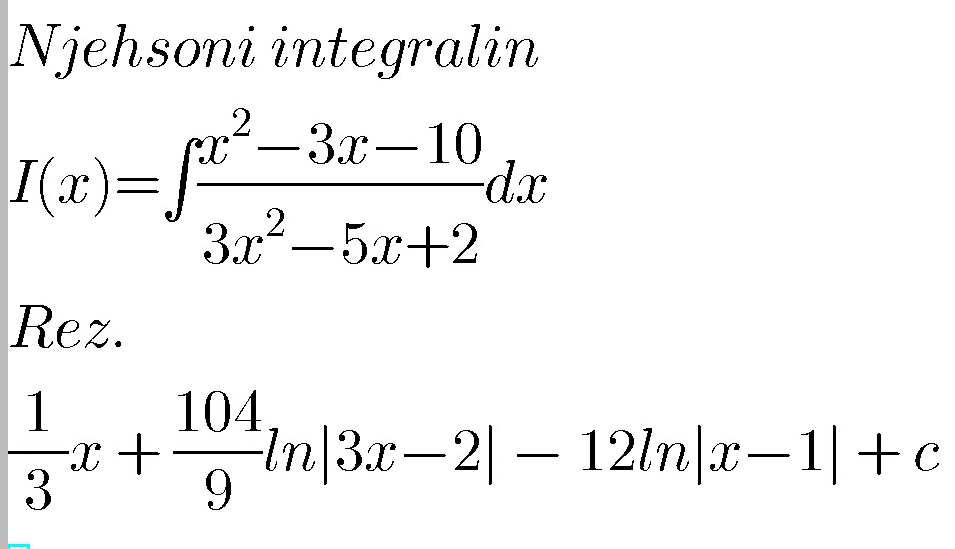
Pg 293 Pg 294 Pg 295 Pg 296 Pg 297 Pg 298 Pg 299 Pg 300 Pg 301 Pg 302
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 298 |
| let give α>0 find the value of ∫_0 ^1 (dx/(√((1−x)(1+αx)))) . |
| find ∫_0 ^∞ (t^n /(e^t −1)) dt by using ξ(x) for n integr ξ(x)=Σ_(n=1) ^∞ (1/n^x ) with x>1 . |
| by using residus theorem prove that ∫_0 ^∞ (t^(a−1) /(1+t)) dt = (π/(sin(πa))) with 0<a<1 . |
| find the value of∫_0 ^∞ (e^(−[t]) /(t+1))dt . |
| calculate ∫_0 ^∞ (x^3 /(1+x^5 ))dx. |
| calculate ∫_0 ^∞ ((1+x^4 )/(1+x^6 )) dx . |
| help ! ! ! ∫ (dx/(csc(x)−1)) = ? [ my way ] ∫( (dx/((1/(sinx)) − 1)) ) =∫((sinx)/(1−sinx)) dx =−∫ ((sinx−1+1)/(sinx−1)) dx =−∫1+(1/(sinx−1)) dx =−(∫1dx+∫((sinx+1)/((sinx−1)(sinx+1))) dx) =−(x+C−∫((sinx+1)/(1−sin^2 x)) dx) =−(x+C−∫ ((sinx)/(cos^2 x)) dx−∫ (1/(cos^2 x)) dx) =−(x+C+∫(cosx)^(−2) dcosx−∫(1/(cos^2 x))dx) =−(x−(cosx)^(−1) +C−∫(1/(cos^2 x))dx) ...and I can′t solve the ∫(1/(cos^2 x))dx oh i just found that is tanx+C |
| find ∫_0 ^∞ ((1−cos(λx))/x^2 ) dx with λ>0 . |
| calculate ∫_0 ^∞ e^(−λx) ((sinx)/(√x)) dx wih λ>0 . |
| let give u_n = ∫_0 ^π ((cos(nx)dx)/(1−2λcosx +λ^2 )) 1) prove that λ u_(n+2) −(1+λ^2 )u_(n+1) +λ u_n =0 2) ptove that Σ u_n is convergent and find its sum |
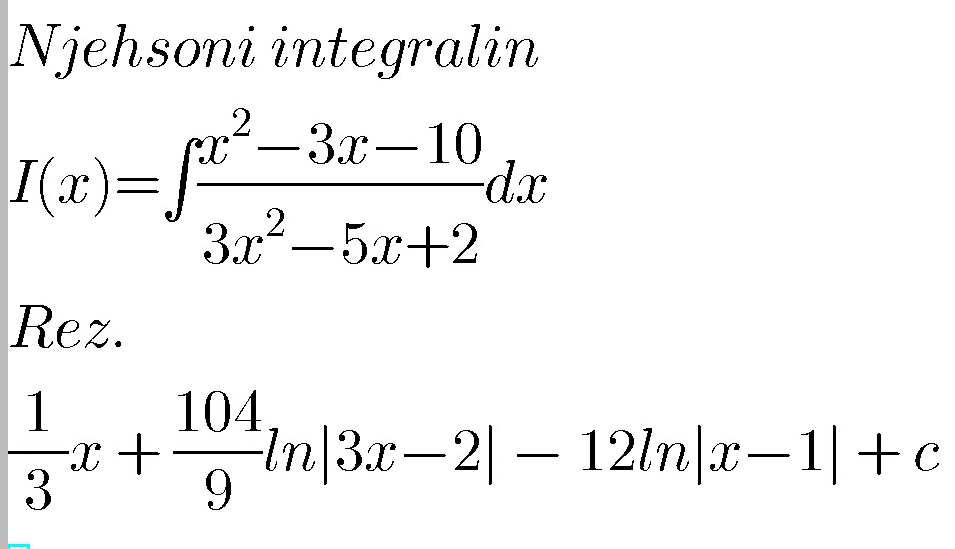
|
| Evaluate ∫((x^4 +1)/(x^6 +1))dx [W.B.H.S 2018] |
| 1) study the convergence of ∫_0 ^1 (x^p /(1+x)) dx 2) find lim_(p→∞) ∫_0 ^1 (x^p /(1+x))dx . |
| plz help Evalute ∫_(π/3 ) ^(π/4) ((sin^2 x)/(√(1−cosx)))dx |
| ∣∫_a ^b f(x)dx≤∣∫_a ^b ∣f(x)∣dx∣ |
| ∫((3x^2 +2x−4)/(7x^2 −9x+2))dx |
|
| find ∫_0 ^1 ((ln(t^2 +2t cosx +1))/t)dt . |
| find∫_0 ^∞ ((ln(x^2 +t^2 ))/(1+t^2 ))dt |
| let f(x)=∫_0 ^∞ (e^(−t) /(1+xt))dt calculate f^((n)) (0). |
| let give 0≤x≤1 calculate ∫_0 ^∞ ((arctan((x/t)))/(1+t^2 )) dt |
| let o≤x≤1 find ∫_0 ^x ((lnt)/(t^2 −1))dt |
| prove that Σ_(n=0) ^∞ (1/((n!)^2 )) =(1/(2π)) ∫_0 ^(2π) e^(2cosx) dx . |
| 1) prove that ∫_0 ^1 ((arctant)/t)dt=−∫_0 ^1 ((lnt)/(1+t^2 ))dt 2) find ∫_0 ^1 ((arctant)/t)dt at form of serie |
| find lim_(n→∞) ∫_0 ^n (cos((x/n)))^n^2 dx. |
| let A_n = ∫_0 ^n (√(1+(1−(x/n))^n )) dt. find a rquivalent of A_n . |
Pg 293 Pg 294 Pg 295 Pg 296 Pg 297 Pg 298 Pg 299 Pg 300 Pg 301 Pg 302 |