Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 300

Question Number 32720 Answers: 0 Comments: 0

find ∫_(−∞) ^(+∞) (dt/(1 +(t+2i)^2 )) .

$f i n d \int_{- \infty}^{+ \infty} \frac{d t}{1 + {(t + 2 i)}^{2}} .$

Question Number 32719 Answers: 0 Comments: 0

cslculate ∫_0 ^∞ (t −[t])e^(−3t) dt .

$c s l c u l a t e \int_{0}^{\infty} (t - [t]) e^{- 3 t} d t .$

Question Number 32718 Answers: 0 Comments: 0

find ∫_0 ^∞ arctan(2x) (e^(−tx) /x) dc with t>0 2) calculate ∫_0 ^∞ ((arctan(2x))/x) e^(−x) dx.

$f i n d \int_{0}^{\infty} a r c t a n (2 x) \frac{e^{- t x}}{x} d c w i t h t > 0$ $2) c a l c u l a t e \int_{0}^{\infty} \frac{a r c t a n (2 x)}{x} e^{- x} d x .$

Question Number 32717 Answers: 0 Comments: 0

finf ∫_0 ^(+∞) (dx/(1+x^2 +x^4 ))

$f i n f \int_{0}^{+ \infty} \frac{d x}{1 + x^{2} + x^{4}}$

Question Number 32716 Answers: 1 Comments: 0

find ∫_0 ^(2π) ((cos^2 x)/(1+3sin^2 x))dx .

$f i n d \int_{0}^{2 π} \frac{{c o s}^{2} x}{1 + 3 {s i n}^{2} x} d x .$

Question Number 32715 Answers: 0 Comments: 1

calculate ∫_(−∞) ^(+∞) (dt/((1+it)(1+it^2 ))) .

$c a l c u l a t e \int_{- \infty}^{+ \infty} \frac{d t}{(1 + i t) (1 + {i t}^{2})} .$

Question Number 32714 Answers: 0 Comments: 1

calculate ∫_1 ^(+∞) (dt/(t^2 (√(1+t^2 )))) .

$c a l c u l a t e \int_{1}^{+ \infty} \frac{d t}{t^{2} \sqrt{1 + t^{2}}} .$

Question Number 32712 Answers: 0 Comments: 1

calculate ∫_0 ^(π/2) (dt/(1+a cos^2 t)) .

$c a l c u l a t e \int_{0}^{\frac{π}{2}} \frac{d t}{1 + a {c o s}^{2} t} .$

Question Number 32722 Answers: 0 Comments: 0

find ∫_0 ^∞ (dx/(1+x^3 )) .

$f i n d \int_{0}^{\infty} \frac{d x}{1 + x^{3}} .$

Question Number 32705 Answers: 0 Comments: 1

let give f(x)= ∫_0 ^∞ ln(1 +(x/t^2 ))dt with ∣x∣<1 find a simple form of f(x).

$l e t g i v e f (x) = \int_{0}^{\infty} l n (1 + \frac{x}{t^{2}}) d t w i t h ∣ x ∣< 1$ $f i n d a s i m p l e f o r m o f f (x) .$

Question Number 32704 Answers: 0 Comments: 0

find ∫_0 ^∞ (((x+1)(√x))/(2+x^2 ))dx.

$f i n d \int_{0}^{\infty} \frac{(x + 1) \sqrt{x}}{2 + x^{2}} d x .$

Question Number 32675 Answers: 1 Comments: 1

Question Number 32708 Answers: 0 Comments: 1

let give f(x)=∫_0 ^(π/2) ((ln(1+xtant))/(tant))dt find a simple form of f(x) 2)calculate ∫_0 ^(π/2) ((ln(1+2tant))/(tant))dt .

$l e t g i v e f (x) = \int_{0}^{\frac{π}{2}} \frac{l n (1 + x t a n t)}{t a n t} d t$ $f i n d a s i m p l e f o r m o f f (x)$ $2) c a l c u l a t e \int_{0}^{\frac{π}{2}} \frac{l n (1 + 2 t a n t)}{t a n t} d t .$

Question Number 32627 Answers: 0 Comments: 1

plzz help ne differentiate between ∫sin(2x)= −(1/2)cox(2x)+c is not change to ∫2sin(x)cos(x) but ∫_b ^a sin(2x)= is change to ∫_b ^a 2sin(x)cos(x)

$p l z z h e l p n e d i f f e r e n t i a t e$ $b e t w e e n$ $\int s i n (2 x) = - \frac{1}{2} c o x (2 x) + c$ $i s n o t c h a n g e t o \int 2 s i n (x) c o s (x)$ $b u t \underset{b}{\int^{a}} s i n (2 x) = i s c h a n g e t o$ $\underset{b}{\int^{a}} 2 s i n (x) c o s (x)$

Question Number 32484 Answers: 0 Comments: 2

∫_1 ^2 ∫_0 ^1 ((ln(x+y))/((x+y))) dx dy

$\int_{1}^{2} \int_{0}^{1} \frac{l n (x + y)}{(x + y)} d x d y$

Question Number 32483 Answers: 0 Comments: 2

calculate ∫_0 ^(2π) (dx/(1+2cosx)) .

$c a l c u l a t e \int_{0}^{2 π} \frac{d x}{1 + 2 c o s x} .$

Question Number 32482 Answers: 0 Comments: 0

find f(x)= ∫_0 ^π ((sin^2 t)/(1−2xcost +x^2 ))dt with ∣x∣<1 .

$f i n d f (x) = \int_{0}^{π} \frac{{s i n}^{2} t}{1 - 2 x c o s t + x^{2}} d t w i t h ∣ x ∣< 1 .$

Question Number 32481 Answers: 0 Comments: 0

find ∫_0 ^∞ ((√(t )) −2(√(t+1)) +(√(t+2))) dt

$f i n d \int_{0}^{\infty} (\sqrt{t} - 2 \sqrt{t + 1} + \sqrt{t + 2)} d t$

Question Number 32480 Answers: 0 Comments: 1

find ∫_0 ^α (√(tanx)) dx with 0<α<(π/2) .

$f i n d \int_{0}^{α} \sqrt{t a n x} d x w i t h 0 < α < \frac{π}{2} .$

Question Number 32479 Answers: 0 Comments: 0

find ∫_0 ^∞ (dx/((x^2 +1)(x^2 +3x +1)))

$f i n d \int_{0}^{\infty} \frac{d x}{(x^{2} + 1) (x^{2} + 3 x + 1)}$

Question Number 32478 Answers: 0 Comments: 1

find ∫_0 ^∞ ln(((1+t^2 )/t^2 ))dt

$f i n d \int_{0}^{\infty} l n (\frac{1 + t^{2}}{t^{2}}) d t$

Question Number 32477 Answers: 0 Comments: 1

calcilate ∫_0 ^1 ((ln(1−x^2 ))/x^2 )dx

$c a l c i l a t e \int_{0}^{1} \frac{l n (1 - x^{2})}{x^{2}} d x$

Question Number 32420 Answers: 0 Comments: 0

Question Number 32419 Answers: 0 Comments: 0

Question Number 32367 Answers: 0 Comments: 0

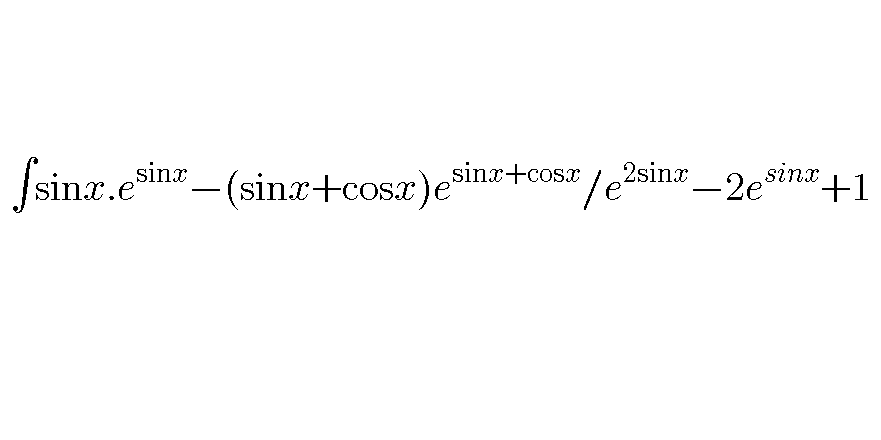
let α∈R and x^2 ≠1 find the value of f(x) = ∫_0 ^π ln(x^2 −2x cost +1)dt calculate f(x).

$l e t α \in R a n d x^{2} \neq 1 f i n d t h e v a l u e o f$ $f (x) = \int_{0}^{π} l n (x^{2} - 2 x c o s t + 1) d t$ $c a l c u l a t e f (x) .$

Question Number 32365 Answers: 0 Comments: 3

let F(x) = ∫_0 ^π ln(1+xcosθ)dθ .with ∣x∣<1 find F(x) .

$l e t F (x) = \int_{0}^{π} l n (1 + x c o s θ) d θ . w i t h ∣ x ∣< 1$ $f i n d F (x) .$

Pg 295 Pg 296 Pg 297 Pg 298 Pg 299 Pg 300 Pg 301 Pg 302 Pg 303 Pg 304

Contact: info@tinkutara.com