
Question and Answers Forum
IntegrationQuestion and Answers: Page 313

Pg 308 Pg 309 Pg 310 Pg 311 Pg 312 Pg 313 Pg 314 Pg 315 Pg 316 Pg 317
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 313 |
| find I_(n,m) = ∫_0 ^1 x^n (1−x)^m dx with (n,m)∈N^★^2 and calculate Σ_(n=0) ^∝ I_(n,m) . |
| let put f(t)=∫_0 ^∞ ((e^(−ax) − e^(−bx) )/x^2 ) e^(−tx^2 ) dx with t≥0 and a>0 and b>0 find a integral form of f(t). |
| Use the trapezoidal rule with 5 ordinates to evaluate ∫_( 0) ^( 0.8) e^x^2 dx |
| Find by the trapezoidal rule the approximate value of ∫_( 0) ^( 1) (dx/(1 + x^2 )). Use ordinates spaced at equal interval of width h = 0.1 |

|
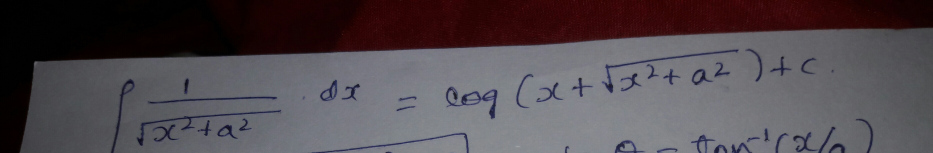
|
| find the value of ∫_0 ^(π/2) (√(tanx))dx . |
| ∫((cos x−cos 2x)/(1−cos x))dx |
| find ∫_1 ^∝ ((arctan(αx))/x^2 ) . |
| calculate ∫_0 ^∝ ((e^(−ax) − e^(−bx) )/x^2 )dx with a>0 b>o |
| find the value of ∫_0 ^1 ((arctan(x +x^(−1) ))/(1+x^2 )) dx |
| find the value of ∫_0 ^∞ (e^(−2x^2 ) /((3+x^2 )^2 ))dx . |
| find ∫ (√(2+tan^2 t)) dt. |
| find ∫ (x^2 /((cosx +x sinx)^2 )) . |
| let give I(x)= ∫_0 ^π ln (1−2x cost +x^2 )dt by using the polynomial p(x)= (z+x)^(2n) −1 find the value of I(x). |
| find the value of A_n = ∫_0 ^π ((sin(nt))/(sint))dt with n∈N^∗ . |
| find the value of F(x)=∫_0 ^(π/2) ((ln(1+x sin^2 t))/(sin^2 t)) dt knowing that −1<x<1 . |
| ∫(√(tan x))dx |
| 1) calculate ∫∫_(]0,1]×]0,(π/2)]) ((dxdy)/(1+(xtany)^2 )) 2) find the value of ∫_0 ^(π/2) (t/(tant))dt . |
| find by two ways the value of ∫∫_([0,1]) x^y dxdxy then calculate ∫_0 ^1 ((t−1)/(lnt))dt . |
| let give A=∫∫_(0≤y≤x≤1) ((dxdxy)/((1+x^2 )(1+y^2 ))) and B= ∫_0 ^(π/4) ((ln(2cos^2 θ))/(2cos(2θ)))dθ calculate A and prove that B=A. |
| find I= ∫∫_D ln(1+x+y)dxdy with D= {(x,y)∈R^2 / x+y≤1 and x≥0 and y≥0 }. |
| calculate I= ∫_0 ^(π/2) (dx/(1+cosx)) and J= ∫_0^ ^(π/2) ((cosx)/(1+cosx))dx . |
| let give f(x)=(√(x+y)) +1 and D={(x,y)∈R^2 / 0≤x≤1 and −1≤y≤1} find the value of ∫∫ f(x,y)dxdy . |
| 1) prove the existence of the integral I=∫_0 ^(π/2) ((ln(1+cosx))/(cosx))dx 2)prove that I= ∫∫_D ((siny)/(1+cosx cosy))dxdy with D=[0,(π/2)]^2 3)find the value of I. |
| let give I_n = ∫_0 ^1 (x^n /(1+x^n ))dx (1) prove that lim_(n−>∝) I_n =0 (2)calculate I_n +I_(n+1) (3) find Σ_(n=1) ^∝ (((−1)^(n−1) )/n) . |
Pg 308 Pg 309 Pg 310 Pg 311 Pg 312 Pg 313 Pg 314 Pg 315 Pg 316 Pg 317 |