Question and Answers Forum

IntegrationQuestion and Answers: Page 315

Question Number 27392 Answers: 0 Comments: 0

Show that the integral: ∫ e^(−x^2 ) dx Can′t be calculated trivially.

$Show that the integral :$ $\int e^{- x^{2}} dx$ ${Can}^{'} t be calculated trivially .$

Question Number 27345 Answers: 0 Comments: 1

prove that ∫_0 ^∞ (t^(x−1) /(e^t −1))dt =ξ(x)Γ(x) with ξ(x)= Σ_(n=1) ^∝ (1/n^x ) and Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt ( x>1)

$p r o v e t h a t \int_{0}^{\infty} \frac{t^{x - 1}}{e^{t} - 1} d t = ξ (x) Γ (x)$ $w i t h ξ (x) = \sum_{n = 1}^{\propto} \frac{1}{n^{x}} a n d Γ (x) = \int_{0}^{\infty} t^{x - 1} e^{- t} d t$ $(x > 1)$

Question Number 27342 Answers: 0 Comments: 1

find f(x)= ∫_0 ^∞ (e^(−x(1+t^2 )) /(1+t^2 )) dt interms ofx with x≥0 and calculate ∫_0 ^∞ e^(−t^2 ) dt .

$f i n d f (x) = \int_{0}^{\infty} \frac{e^{- x (1 + t^{2})}}{1 + t^{2}} d t i n t e r m s o f x$ $w i t h x ⩾ 0 a n d c a l c u l a t e \int_{0}^{\infty} e^{- t^{2}} d t .$

Question Number 27341 Answers: 0 Comments: 0

prove that ∫_0 ^∞ e^(−(t^2 +(1/t^2 ))) dt is convergeny and find its value .

$p r o v e t h a t \int_{0}^{\infty} e^{- (t^{2} + \frac{1}{t^{2}})} d t i s c o n v e r g e n y$ $a n d f i n d i t s v a l u e .$

Question Number 27309 Answers: 1 Comments: 0

find the value of ∫_0 ^∝ (((−1)^([x]) )/((2x+1)^2 ))dx

$f i n d t h e v a l u e o f \int_{0}^{\propto} \frac{{(- 1)}^{[x]}}{{(2 x + 1)}^{2}} d x$

Question Number 27282 Answers: 0 Comments: 1

∫log(2+x^2 )dx

$\int l o g (2 + x^{2}) d x$

Question Number 27271 Answers: 1 Comments: 0

Proof ∫(1/(a^2 −x^2 ))dx =(1/(2a))ln∣((a+x)/(a−x))∣+c

$P r o o f$ $\int \frac{1}{a^{2} - x^{2}} d x = \frac{1}{2 a} l n ∣ \frac{a + x}{a - x} ∣ + c$

Question Number 27215 Answers: 1 Comments: 0

find the value of ∫_(−1) ^1 (dx/((√(1−x^2 )) +(√(1+x^2 )))) .

$f i n d t h e v a l u e o f \int_{- 1}^{1} \frac{d x}{\sqrt{1 - x^{2}} + \sqrt{1 + x^{2}}} .$

Question Number 27187 Answers: 0 Comments: 1

find I= ∫_0 ^∝ ((cosx)/(cosh(x)))dx

$f i n d I = \int_{0}^{\propto} \frac{c o s x}{c o s h (x)} d x$

Question Number 27186 Answers: 1 Comments: 1

find I=∫_0 ^π (dx/(cosx +2sinx)) .

$f i n d I = \int_{0}^{π} \frac{d x}{c o s x + 2 s i n x} .$

Question Number 27185 Answers: 0 Comments: 0

find ∫∫_D (x+y)^2 e^(x^2 −y^2 ) dxdy with D={(x,y)∈R^(2 ) /0<x<1 and 0<y<1−x }.

$f i n d \int \int_{D} {(x + y)}^{2} e^{x^{2} - y^{2}} d x d y w i t h$ $D = {(x, y) \in R^{2} / 0 < x < 1 a n d 0 < y < 1 - x} .$

Question Number 27184 Answers: 0 Comments: 1

calculate in terms of x f(x)= ∫_0 ^(π/(2 )) (dt/(1+xsint)) .

$c a l c u l a t e i n t e r m s o f x f (x) = \int_{0}^{\frac{π}{2}} \frac{d t}{1 + x s i n t} .$

Question Number 27183 Answers: 1 Comments: 0

find the value of I= ∫_0 ^1 ((t−1)/(lnt))dt .

$f i n d t h e v a l u e o f I = \int_{0}^{1} \frac{t - 1}{l n t} d t .$

Question Number 27182 Answers: 0 Comments: 1

find the value of I_a = ∫∫_D_a e^(−((x^2 +y^2 )/2)) dxdy with D_a ={(x,y)∈R^2 / x^2 +y^2 ≤ a^2 }

$f i n d t h e v a l u e o f I_{a} = \int \int_{D_{a}} e^{- \frac{x^{2} + y^{2}}{2}} d x d y w i t h$ $D_{a} = {(x, y) \in R^{2} / x^{2} + y^{2} ⩽ a^{2}}$

Question Number 27083 Answers: 1 Comments: 0

∫3x^2 /x^6 +1

$\int 3 x^{2} / x^{6} + 1$

Question Number 27045 Answers: 0 Comments: 0

find the value of ∫_(2/π) ^(6/π) x^3 cos([(1/x)])dx

$f i n d t h e v a l u e o f \int_{\frac{2}{π}}^{\frac{6}{π}} x^{3} c o s ([\frac{1}{x}]) d x$

Question Number 27032 Answers: 0 Comments: 1

xy=(1−x^2 )(dy/dx) x=0 y=1

$x y = (1 - x^{2}) \frac{d y}{d x} x = 0 y = 1$

Question Number 27031 Answers: 1 Comments: 0

xy=(1−x^2 )(dy/dx) x=0 y=1

$x y = (1 - x^{2}) \frac{d y}{d x} x = 0 y = 1$

Question Number 27003 Answers: 0 Comments: 2

∫_(1/8) ^(1/2) ⌊ln ⌈(1/x)⌉⌋ dx

$\underset{1 / 8}{\int^{1 / 2}} ⌊ \ln ⌈ \frac{1}{x} ⌉ ⌋ d x$

Question Number 26993 Answers: 0 Comments: 5

Question Number 26781 Answers: 1 Comments: 4

Question Number 26759 Answers: 1 Comments: 1

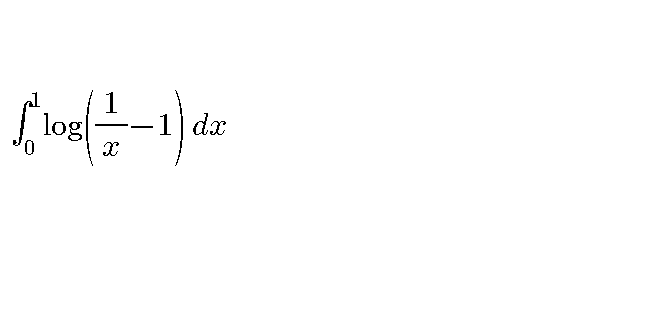
find the value of ∫_0 ^( ∝) (dx/((x+1)(x+2)(x+3))) .

$f i n d t h e v a l u e o f \int_{0}^{\propto} \frac{d x}{(x + 1) (x + 2) (x + 3)} .$

Question Number 26758 Answers: 0 Comments: 1

let give D={( x,y )∈R^2 /x^2 −x +y^2 ≤ 4 and 0≤y≤1} calculate ∫∫_D ln(xy)(√( x^2 +y^2 dxdy ))

$l e t g i v e D = {(x, y) \in R^{2} / x^{2} - x + y^{2} ⩽ 4 a n d 0 ⩽ y ⩽ 1}$ $c a l c u l a t e \int \int_{D} l n (x y) \sqrt{x^{2} + y^{2} d x d y}$

Question Number 26757 Answers: 0 Comments: 3

give the decomposition of F(x) = (1/(x^(2n) +1)) inside C[x] then find the value of ∫_0 ^∞ (dx/(1+x^(2n) )) n∈N and n≠o

$g i v e t h e d e c o m p o s i t i o n o f F (x) = \frac{1}{x^{2 n} + 1} i n s i d e C [x]$ $t h e n f i n d t h e v a l u e o f \int_{0}^{\infty} \frac{d x}{1 + x^{2 n}} n \in N a n d n \neq o$

Question Number 26756 Answers: 0 Comments: 2

prove that ∫_0 ^1 (dx/(x+ e^x )) = Σ_(n=0) ^∝ (((−1)^n )/((n+1)^(n+1) )) A_n with A_n = ∫_0 ^(n+1) t^n e^(−t) dt .

$p r o v e t h a t \int_{0}^{1} \frac{d x}{x + e^{x}} = \sum_{n = 0}^{\propto} \frac{{(- 1)}^{n}}{{(n + 1)}^{n + 1}} A_{n}$ $w i t h A_{n} = \int_{0}^{n + 1} t^{n} e^{- t} d t .$

Question Number 26755 Answers: 1 Comments: 0

find ∫ (dx/(x^6 −1)) .

$f i n d \int \frac{d x}{x^{6} - 1} .$

Pg 310 Pg 311 Pg 312 Pg 313 Pg 314 Pg 315 Pg 316 Pg 317 Pg 318 Pg 319

Contact: info@tinkutara.com