
Question and Answers Forum
IntegrationQuestion and Answers: Page 319



Pg 314 Pg 315 Pg 316 Pg 317 Pg 318 Pg 319 Pg 320 Pg 321 Pg 322 Pg 323
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 319 |
| answer to 25955.we introduce the parametric function F(t) =∫_0 ^∞ ln(1+(1+x^2_ )t)(1+x^2 )^(−1) dx after verifying that F is derivable on[0.∝[ we find ∂F/∂t= ∫_0 ^∞ ( (1+(1+x^2 )t)^(−1) dx ∂F/∂t=1/2 ∫_R (tx^2 +t+1)^(−1) dx we put f(z) =(tz^2 +z+1)^(−1) let find the poles of f..tz^2 +z+1=0 <−> z=+−i((t+1)t^(−1) )^(1/2) and the poles are z_0 =i((t+1)t^(−1) )^(1/2) and z_1 =−i((t+1)t^(−1) )^(1/2) and f(t) =(t(t−z_0 )(t−z_1 ))^(−1) by residus theorem ∫_R f(z)dz =2iπ R(f.z_0 ) =2iπ (t(z_0 −z_1 ))^(−1) =π t^(−1/2) (t+1)^(−1/2 ) −>∂F/∂t =π 2^(−1) t^(−1/2) (1+t)^(−1/2) −>F(t) =π 2^(−1 ) ∫_0 ^t x^(−1/2) (1+x)^(−1/2) dx +α α=F(0)=0 and F(t) =π2^(−1) ∫_0 ^t x^(−1/2) (1+x)^(−1/2) dx and by the changement x^(1/2) =u we find F(t) = π ln( t^(1/2) +(1+t)^(1/2) ) so ∫_0 ^∞ ln(2+x^2 )(1+x^2 )^(−1) dx=F(1)=πln(1+2^(1/2) ) |
| find the value of ∫_0 ^∞ ln(2+x^2 )(1+x^2 )^(−1) dx |
| answer to 25824 we have a^(−x^2 ) = e^(−x^2_ ln(a)) so for a>1 ln(a)=( (ln(a))^(1/2) )^2 >>>>∫_R a^(−^ x^2 ) = ∫_R e^(−(x (ln(a)^(1/2) )^2 ) dx and with the changement t=x (ln(a)^(1/2) >>>>x=t ( ln(a))^(−1/2) we have ∫_R a^(−x^2 ) dx = π^(1/2) (ln(a))^(−1/2) ...if 0<a<1 ln(a)<0 and the integrale is divergente... |

|

|
| find the value of integral ∫_R (z−a)^(−1) dz with a from C aplly this result to find the value of ∫_0 ^∞ (2 +x^4_ )^(−1) dx. |
| ∫((2+2x)/((x−1)(x^2 +1)))dx |
| ∫(x^n lnx)dx |
| if ∫_R e^(−x^2 ) dx = π^(1/2) find value of ∫_R a^(−x^2_ ) dx with a>0 and a not 1. |
| answer to q25796 f_ ind the value off(x)= ∫_0^ ^π_ ln(1+xcosθ)dθ with 0<x<1 ∂f/∂x= ∫_0 ^π cosθ(1+xcosθ)^(−1) dθ=πx^(−1) −x^(−1) ∫_0 ^π (1+xcosθ)^(−1) dθand by the changeent tanθ=u then the changement u=((1+x)(1+x)^(−1^ ) )^ .t.we find ∫_0 ^θ (1+xcosθ)^(−1) dθ =π(1−x^2_ )^(−1/2) so ∂f/∂x=πx^(−1) −πx^(−1) (1−x^(−1/2) ) so f(x)= π ln(x)−π∫^x t^(−1) (1−t^2 )^(−1/2) dt but ∫^x t^(−1) (1−t^2 )dt=−1. 2^(−1) ln((1+(1−x^2 )^(1/2) .(1−(1−x^2 )^(1/2) )^(−1) ) and f(x)=πln(x)+π.2^(−1) ln( (1+(1−x^2 )^(1/2) ((1−(1−x^2 )^(1/2) )^(−1) +β β=f(1)=∫_0 ^(π=) ln(1+cosθ)dθ=−πln(2) so ∫_0 ^π (1+xcosθ)dθ = πlnx +π2^(−1) ln((1+(1−x^2 )^(1/2^ ) )((1−(1−x^2 )^(1/2) )^(−1) −πln(2). |

|
| find the value of f(x)=∫_0^ ^π ln( 1+xcosθ)dθ with 0<x<1 |
|
| ∫(1/(sin x+cos x))dx |
| a−nser to question 25765...we put I=∫_0 ^∞ (cos(x^(2n) )(1+x^2 )^(−1) dx and J=∫_0 ^∞ sin(x^(2n) )(1+x^2 )^(−1) dx...we have 2(I+iJ)=∫_R e^(ix^(2n) ) (1+x^2 )^(−1) dx...let f(z)=e^(ix^(2n) ) (1+x^2 )^(−1) by residus therem ∫_R f(z)dz = 2iπRes(f.i) but Res(f.i)= lim_(z−i) (z−i)f(z)=e^(i(i)^(2n) ) = e^(i(−1)_ ^n ) (2i)^(−1) then ∫_R f(z)dz = πe^((−1)^n ) = π( cos(−1)^n +isin(−1)^n ) then ∫_0 ^∞ cos(x^(2n) )(1+x^2 )^(−1) dx =π2^(−1) cos(−1)^n and ∫_0 ^∞ sin(x^(2n) )(1+x^2 )^(−1) dx=π.2^(−1) sin(−1)^n_ <>.... |
| find the value of ∫_0 ^∞ cos(x^(2n) )(1+x^2 )^(−1) dx and ∫_0 ^∞ sin( x^(2n) )^ (1+x^2 )^(−1) dx |
| find the value of∫_0 ^∞ artan(2x)(1+x^2 )^(−1_ ) the key of slution put F(t)=∫_0 ^∞ artan(xt)(1+x^2 )^(−1) find ∂F/∂t first then F(t) and take t=2 you will of find find the value of integral.. |
| find the value of ∫_0 ^∞ sin(x^n )( 1 + x^2 )^(−1) dx |
| we give ∫_0 ^∞ t^(a−1) (1 + t)^(−1) dt =π (sin(πa))^(−1) with 0<a<1 find the value of ∫_0 ^∞ (1 +x^(16) )^(−1) dx |
| let 0<x<1 find the value of F(x) = ∫ ln (1+x cost)dt fromt=0 to t=pi |
| find the value of ∫_0 ^∞ sin(x^ n )/x^ 2 + 1 dx |
| find the value of ∫_0 ^(∝ ) ((ln(1+t^2 ))/(1−t^2 )) dt |
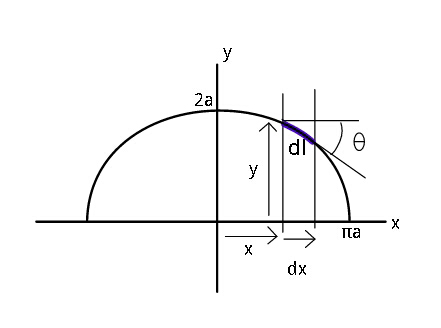
| find the value of ∫∫_D (x^2 /y^2 ) dxdy with D ={(x ,y)∈R^2 / 1≤x≤2 and (1/x)≤y≤ x }. |

|
| ∫_6 ^5 f(x)dx |
| ∫_0 ^1 ((6x^2 − x − 1)/(6x^2 − 5x + 1)) dx |
Pg 314 Pg 315 Pg 316 Pg 317 Pg 318 Pg 319 Pg 320 Pg 321 Pg 322 Pg 323 |