
Question and Answers Forum
IntegrationQuestion and Answers: Page 322



Pg 317 Pg 318 Pg 319 Pg 320 Pg 321 Pg 322 Pg 323 Pg 324 Pg 325 Pg 326
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 322 |
| ∫_0 ^(π/2) sin^2 xcos^3 xdx |
| ∫sin^5 θdθ |
| ∫_(π/6) ^(π/3) (1/2)cot^2 2θdθ |
| ∫_(π/6) ^(π/3) 1/2cot^2 2θdθ |
| ∫2cot^2 2t |
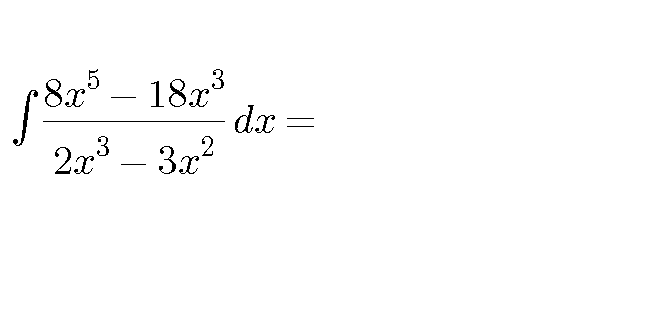
|
| ∫((secθ dθ)/(1−secθ)) |
| ∫(√(secθ)) dθ |
| ∫3tan2t |
| ∫_0 ^(0.5) 2tan^2 2tdt |
| 5cos^5 tsin t |
| 3sec^2 3xtan3x |
| ∫_(π/2) ^(π/4) (3x+7) |

|
| ∫_0 ^1 ((x^7 − 1)/(ln x)) dx |

|

|
| integrate with respect to x ∫(dx/(9x^2 +6x+10)) |
| integrate with respect to x ∫x^(sinx) |
| Demostration of the volume of an sphere V=((4πr^3 )/3) x^2 +y^2 +z^2 =r^2 We divide the sphere in 8 parts. So the volume of a part is ∫_0 ^( r) ∫_0 ^( (√(r^2 −x^2 ))) (√(r^2 −x^2 −y^2 ))∂y∂x Lets asumme a^2 =r^2 −x^2 ∫_0 ^( r) ∫_0 ^( a) (√(a^2 −y^2 ))∂y∂x ∫_0 ^( r) a∫_0 ^( a) (√(1−((y/a))^2 ))∂y∂x Lets assume (y/a)=sinθ⇒(∂y/a)=cosθ∂θ ∫(√(1−sin^2 θ))acosθ∂θ ∫acos^2 θ∂θ a((θ/2)−((sin2θ)/4)) a(((arcsin((y/a)))/2)−((y(√(a^2 −y^2 )))/(2a^2 ))) ∫_0 ^( r) a^2 (((arcsin((y/a)))/2)−((y(√(a^2 −y^2 )))/(2a^2 )))∣_0 ^a ∂x ∫_0 ^( r) (((a^2 arcsin((y/a))−y(√(a^2 −y^2 )))/2))∣_0 ^a ∂x ∫_0 ^( r) ((πa^2 )/4)∂x ∫_0 ^( r) ((π(r^2 −x^2 ))/4)∂x (((6πr^2 x−2πx^3 )/(24)))∣_0 ^r ((πr^3 )/6)=1/8Volume of the sphrere so... V=((4πr^3 )/3) |
| integrate with respect to x ∫(((2x+1)/(x^2 +4x+8)))dx |
| ∫e^x^2 dx |
| ∫_1 ^5 (e^x /x^2 ) dx |
| ∫ (√(sin x)) + (√(cos x)) dx |
| Find the volume of the solid of revolution obtained by revolving area bounded by x = 4 + 6y − 2y^2 , x = −4, x = 0 about the y−axis |
| ∫(tanx)^(1/3) dx |
Pg 317 Pg 318 Pg 319 Pg 320 Pg 321 Pg 322 Pg 323 Pg 324 Pg 325 Pg 326 |