
Question and Answers Forum
IntegrationQuestion and Answers: Page 327



Pg 322 Pg 323 Pg 324 Pg 325 Pg 326 Pg 327 Pg 328 Pg 329 Pg 330 Pg 331
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 327 |
| ∫ ((d((√(3x))))/(√((√x) + 7))) |
| ∫dx/x(√(x^4 −1)) |
| ∫(√(1+x^4 )) dx please solve this question. |
| ∫ ((sin x)/(1 + cos^2 x)) dx |
| ∫ (√(1 + (1/x^2 ) + (1/((x + 1)^2 )))) dx |

|
| ∫ ((x + sinx)/(cosx)) dx |
| ∫_0 ^5 (1/(∫_1 ^8 e^x^(−5) ))dx |
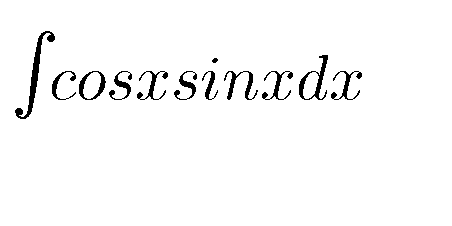
|
| If y = (√(x^2 + (√(x^2 + (√(x^2 + (√(...)))))))) find ∫(y + (√y)) dx |
| If f(x) = (√(x^2 (√(3(√(x^2 (√(3(√)...)))))))) find ∫ f(x) dx |
| ∫cos2x ln(1+tanx)dx |
| prove that ∫_0 ^( π) ((x tanx)/(tanx+secx))dx=(π/2)(π−2) |
| show that ∫_0 ^(π/4) ((x sinx)/(1+cos^2 x))dx=(π/4) |
| (a) Evaluate the integral of the function: y(x) = ((3x + 1)/(2x^2 − 2x + 3)) (b) Find the constant A, B, C in the identity: ((3x^2 − ax)/((x − 2a)(x^2 + a^2 ))) ≡ (A/((x − 2a))) + ((Bx + Ca)/((x^2 + a^2 ))) where a is a constant, hence prove that. ∫_0 ^( 2) ((3x^2 − ax)/((x − 2a)(x^2 + a^2 ))) dx = (π/4) − (3/2) ln(2) |

|
| Please answer Q. 17525 |
| evaluate; ∫ln (sin 2x)dx |

|
| Find the fourier series of : f(x) = x, from 0 < x < π |
| ∫_( 0) ^( n) x^2 (n − x)^p dx for p > 0 |
| a particle starts with an initial speed u,it moves in a straight line with an accleration which varies as the square of the time the particle has been in motion. Find the speed at any time t,and the distance travelled. |
| ∫_( 0) ^( a/2) x^2 (a^2 − x^2 )^(3/2) dx |
| Evaluate ∫_(−1) ^1 (1−x^2 )^(n/2) dx for n ∈ Z∩[0;∞) (i.e. 0, 1, 2, ...) and: a) n ≡ 0(mod 2) b) n ≡ 1(mod 2) |
| ∫(dx/(sin^5 x+cos^5 x)) |
| S(n)=∫_0 ^1 x^(2n) sin(2nπx)dx |
Pg 322 Pg 323 Pg 324 Pg 325 Pg 326 Pg 327 Pg 328 Pg 329 Pg 330 Pg 331 |