
Question and Answers Forum
IntegrationQuestion and Answers: Page 36




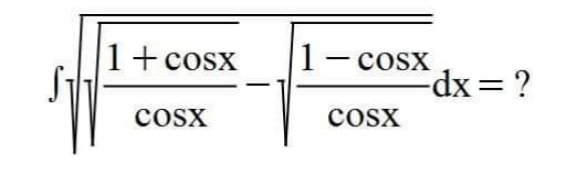


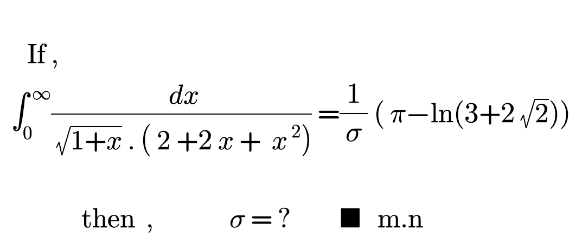






|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 36 |

|

|
| find the value of b so that the line y=b divides the region bound by the graphs of the two functinos , into two regions of equal area. f(x)=9−x^2 and g(x)=0 |

|

|
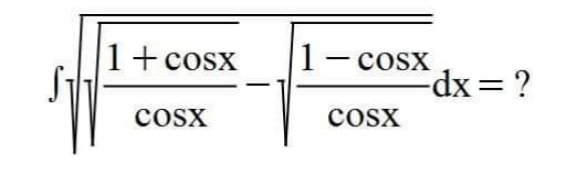
|

|
| 𝛗 = ∫_0 ^( ∞) ((cos (ax)− sin(bx))/x^( 2) )dx =? 𝛗=∫_0 ^( ∞) ((1−2sin^( 2) (((ax)/2))−(1−2sin^( 2) (((bx)/2))))/(x^2 ))dx =2 {∫_0 ^( ∞) (((sin(((bx)/2)))/x))^2 dx=Θ_1 }−2{∫_0 ^( ∞) (((sin(((ax)/2)))/x))^2 dx=Θ_2 } Θ_( 1) =^(((bx)/2)=t) (b/2)∫_0 ^( ∞) ((sin^( 2) (t))/t^( 2) )dt= ((πb)/4) similarly : Θ_( 2) =((πa)/4) ∴ 𝛗= (π/2)(∣b∣−∣a∣) Dirichlet′s integrals: ∫_0 ^( ∞) ((sin(x))/x)dx=(π/2)=∫_0 ^( ∞) ((sin^2 (x))/x^( 2) )dx |
| prove that ∫_0 ^( ∞) (( sin(x))/(sinh(x))) dx = (π/2)tanh((π/2)) |

|
| let ∀n∈N: I_n (f(x))= the n^(th) antiderivate of f(x) with I_0 =f(x) find the formula for the constants a_n , b_n of I_n (ln x)=a_n x^n ln x +b_n x^n |
| ∫_0 ^( ∞) (( dx)/( (√(1+x)) .(2+2x +x^( 2) )))=(1/σ) (π−ln(3+2(√3) )) σ = ? −− solution −− Ω=^((√(1+x)) =t) 2∫_0 ^( ∞) (dt/( 1+ t^( 4) )) = 2∫_0 ^( 1) (dt/(1 + t^( 4) )) Ψ = ∫_0 ^( 1) (( dt)/(1+t^( 4) )) = (1/2)∫_0 ^( 1) (( 1+t^( 2) −(t^( −2) −1))/(1+t^( 4) ))dt = (1/2) ∫_0 ^( 1) (( 1+ t^( 2) )/(1+t^( 4) )) dt +(1/2) ∫_0 ^( 1) ((1−t^( 2) )/(1+ t^( 4) )) dt Φ=∫_0 ^( 1) ((1 +t^( 2) )/(1+t^( 4) ))dt =∫_0 ^( 1) (( t^( −2) +1)/(t^( −2) + t^( 2) )) dt =∫_0 ^( 1) (( 1+t^( −2) )/(( t^ − t^( −1) )^( 2) +2)) =^(sub) [ (1/( (√2))) tan^( −1) (t −t^( −1) )]_0 ^1 =(π/(2(√2))) ∗ 𝛗 = ∫_0 ^( 1) (( 1−t^( 2) )/(1+t^( 4) )) dt = ∫_0 ^( 1) ((t^( −2) −1)/(( t +t^( −1) )^( 2) −2))dt =^(t +(1/t) =u) −∫_2 ^( ∞) (du/(( u−(√2) )(u+ (√2) ))) = ((−1)/(2(√2))) [ln(((u −(√2))/(u+(√2))))]_2 ^( ∞) =(1/(2(√2))) ln(((2−(√2))/(2+(√2))) ) 𝛗 =−(1/(2(√2))) ln( 3 +2(√2) ) ∗∗ (∗) & (∗∗):: Ω=2Ψ= (Φ + 𝛗) =(1/(2(√2))) ( π −ln( 3 +2(√2) ) ...■m.n |
| ∫_0 ^1 ^n (√x) (arcsin x) dx |
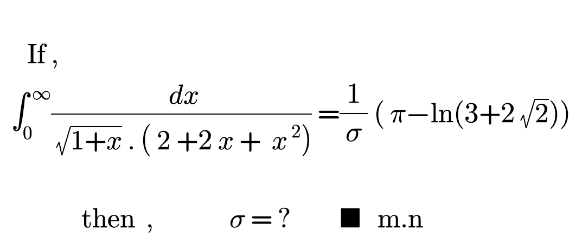
|

|

|
| let U_n =∫_0 ^1 (√(1−x^n ))ln^2 xdx 1)lim U_n ? 2)equivalent of U_n (n→∞) |
| Refer to Q181319 ∫((x^4 +1)/(x^4 +x+2))dx ((x^4 +1)/(x^4 +x+2))=1+(x/(2(x^2 +x+1)))−(x/(2(x^2 −x+1))) =1+(1/4)[(((2x+1)−1)/(x^2 +x+1))−(1/4)×(((2x−1)+1)/((x^2 −x+1))) =(1/4)×[log(x^2 +x+1)]^′ −(1/4)×((1/([((√3)/2)(x+(1/2))^2 ]+1))) −((1/4)[log(x^2 −x+1)]^′ +(1/4)((1/([((√3)/2)×(x−(1/2)]^2 +1)))) first with [((√3)/2)( x+(1/2))]=u ∫(1/(u^2 +1))du=arctg(u) and v=[((√3)/2)(x−(1/2) )]=v ∫(dv/(1+v^2 ))=arctg(v) ............... |
| find ∫_0 ^1 (√(1−x^4 ))lnx dx |

|
| ∫∫_d dxdy x=y^2 −1 x=1−y D=? |
| ∫_0 ^∞ e^(−e^x ) (√x) dx=? |
| lim_( x→ 0^+ ) (x^( (1/(ln(xsin(x^3 ))))) )=? |

|

|

|