|
|

|
All Questions Topic List |
IntegrationQuestion and Answers: Page 39 |
Question Number 170501 Answers: 1 Comments: 0
|
| solve this:
∫∫_D x^2 e^(xy) dxdy
D:{(x.y)∈R^2 /0≤x≤1. 0≤y≤2}
∫∫_D ((ydxdy)/((1+x^2 +y^2 )^(3/2) )). 0≤x≤1.0≤y≤1.
|
|
Question Number 170475 Answers: 0 Comments: 0
|
|
An easy question of Measure theory:
Prove that : μ ( Q )=0 ■m.n
|
|
Question Number 170388 Answers: 0 Comments: 0
|

|
Question Number 170384 Answers: 0 Comments: 0
|
| Prove that
∫_0 ^( (π/2)) ln(a−sin^2 (x))dx=πln((√((a−1)/a))+1)+(π/2)ln((a/4))
a>0 Im{a}≠0
|
|
Question Number 170368 Answers: 0 Comments: 0
|

|
Question Number 170349 Answers: 1 Comments: 0
|
|
help please
∫_1 ^∞ ((1/t)−sin^(−1) ((1/t))) dt
I can show that it is equal to
−Σ_(n≥0) (−1)^n (((2n−1)!)/(4^n (n!)^2 (2n+1)))
but I cant calculate it...
|
|
Question Number 170189 Answers: 0 Comments: 2
|
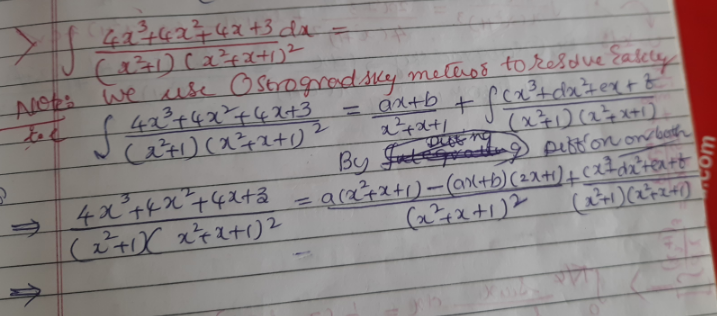
|
Question Number 170255 Answers: 1 Comments: 0
|
| (d/dx)[∫_2 ^x e^t^2 dt=?
|
|
Question Number 170109 Answers: 0 Comments: 0
|

|
Question Number 169930 Answers: 0 Comments: 0
|
| find f(α)=∫_0 ^1 ((arctan(αx))/(1+x^2 ))dx
|
|
Question Number 169906 Answers: 0 Comments: 0
|
| Evaluate ∫∫e^(2x+3y) dxdy over the triangle
bounded by the lines x = 0, y = 0, x+y = 1.
|
|
Question Number 169873 Answers: 2 Comments: 0
|
| ∫_0 ^1 ((ln(1+x))/x)dx=?
|
|
Question Number 169864 Answers: 1 Comments: 0
|

|
Question Number 169825 Answers: 1 Comments: 0
|
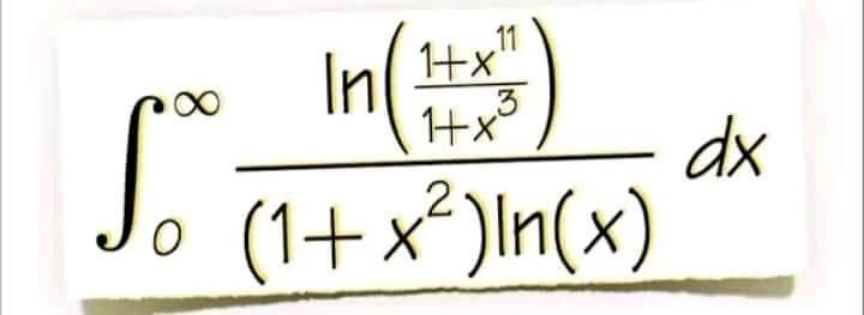
|
Question Number 169706 Answers: 0 Comments: 0
|
| using cylindrical coordinates { ((x=rcosθ)),((y = rsin θ)),((z=z)) :}
to evaluate the integral
K= ∫∫∫_S (√(x^2 +y^2 −z^2 )) dxdydz
where
S= {(x,y,z) ∈R^3 : x^2 +y^2 ≤ 4, 0 ≤z≤(√(x^2 +y^2 ))}
|
|
Question Number 169677 Answers: 2 Comments: 0
|
| M = ∫ (dx/((x−4)(√(x^2 −6x+8)))) =?
|
|
Question Number 169654 Answers: 2 Comments: 0
|
| ∫_0 ^1 ((3x^3 −x^2 +2x−4)/( (√(x^2 −3x+2)))) dx = ?
|
|
Question Number 169563 Answers: 0 Comments: 1
|

|
Question Number 169559 Answers: 1 Comments: 1
|
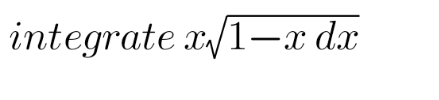
|
Question Number 169548 Answers: 0 Comments: 1
|
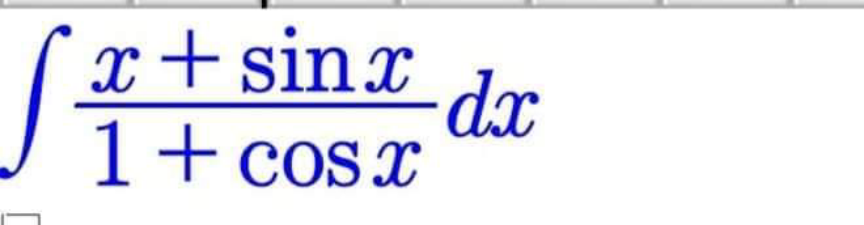
|
Question Number 169504 Answers: 0 Comments: 1
|
|
Question Number 169421 Answers: 0 Comments: 0
|

|
Question Number 169268 Answers: 1 Comments: 0
|
| 𝛀=∫((cos^2 (ln(tan(x/2))))/(tan((x/2))))dx=?
|
|
Question Number 169259 Answers: 0 Comments: 1
|

|
Question Number 169230 Answers: 1 Comments: 0
|
|
Question Number 169169 Answers: 0 Comments: 3
|

|
Pg 34
Pg 35
Pg 36
Pg 37
Pg 38
Pg 39
Pg 40
Pg 41
Pg 42
Pg 43
|
Terms of Service |
Privacy Policy |
Contact: info@tinkutara.com |