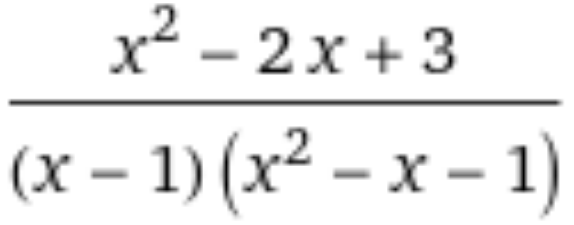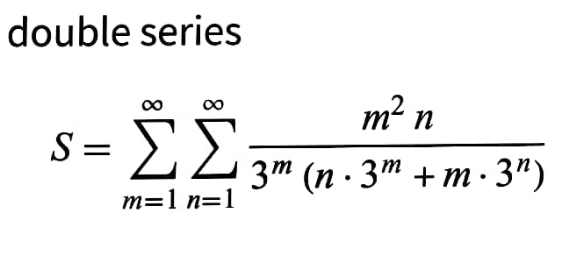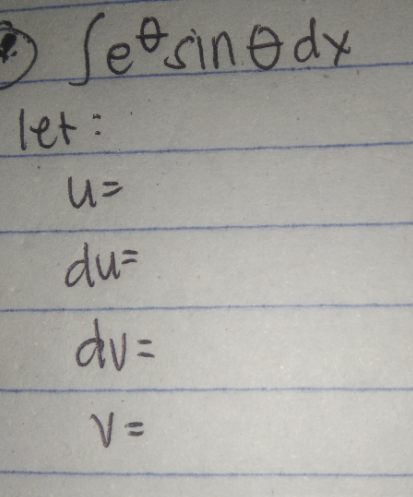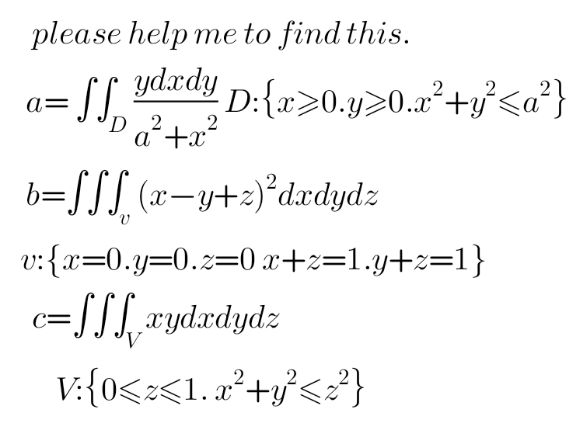Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 40

Question Number 171371 Answers: 3 Comments: 0

∫_(−∞) ^(+∞) (dx/(1+x^4 ))=?

$\int_{- \infty}^{+ \infty} \frac{d x}{1 + x^{4}} = ?$

Question Number 171367 Answers: 0 Comments: 0

Question Number 171301 Answers: 0 Comments: 1

∫_1 ^2 6x^2 −2x+3

$\int_{1}^{2} 6 x^{2} - 2 x + 3$

Question Number 171260 Answers: 1 Comments: 0

Change to polar coordinates: ∫^( 4a) _0 ∫_(y^2 /4a) ^a (((x^2 −y^2 )/(x^2 +y^2 ))) dx dy

$\underset{―}{C h a n g e t o p o l a r c o o r d i n a t e s :}$ ${\int_{0}}^{4 a} \int_{y^{2} / 4 a} \overset{a}{} (\frac{x^{2} - y^{2}}{x^{2} + y^{2}}) d x d y$

Question Number 171253 Answers: 2 Comments: 0

Question Number 171213 Answers: 0 Comments: 0

In electricity, the electrostatic field is defined as: E = ∫_0 ^π [((a^2 σ sin θ)/(2ε(√(a^2 −x^2 −2ax cosθ))))]dθ where a,σ and ε are constants. Consider that x>a and show that E= ((a^2 σ)/(εx))

$In electricity, the electrostatic field$ $is defined as :$ $E = \int_{0}^{π} [\frac{a^{2} σ \sin θ}{2 ϵ \sqrt{a^{2} - x^{2} - 2 a x \cos θ}}] d θ$ $where a, σ and ϵ are constants . Consider$ $that x > a and show that E = \frac{a^{2} σ}{ϵ x}$

Question Number 171198 Answers: 1 Comments: 0

evaluate ∫_0 ^( π) log (a+cos x)dx

$e v a l u a t e$ $\int_{0}^{π} \log (a + \cos x) d x$

Question Number 171171 Answers: 1 Comments: 2

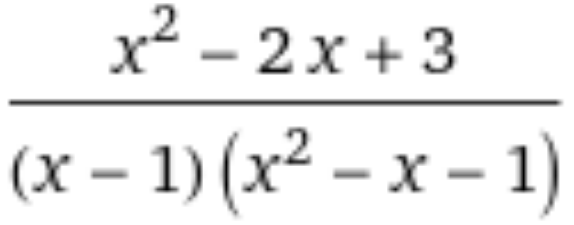
Question Number 171130 Answers: 0 Comments: 0

Question Number 171125 Answers: 1 Comments: 0

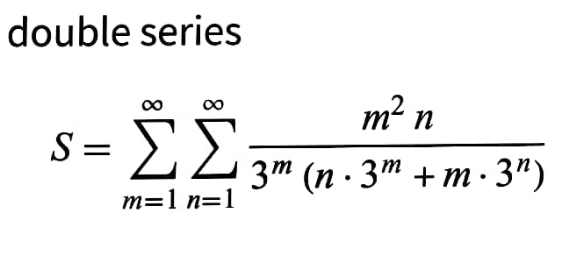
Question Number 171117 Answers: 3 Comments: 0

∫_0 ^∞ ((sin x)/x)dx = (?)

$\underset{0}{\int^{\infty}} \frac{s i n x}{x} d x = (?)$

Question Number 171108 Answers: 1 Comments: 0

Question Number 171096 Answers: 1 Comments: 0

∫((x e^(2x) )/((2x+1)^2 ))dx please help

$\int \frac{x e^{2 x}}{{(2 x + 1)}^{2}} d x p l e a s e h e l p$

Question Number 171090 Answers: 1 Comments: 3

I_n =∫_0 ^1 (1−u)(√(ud(u))) Demonstrate that ∀n∈N, I_(n+1) −I_n =(1−u)^n u^(3/2) d(u) and deduce the meaning of variations of (I_n )∈N

$I_{n} = \int_{0}^{1} (1 - u) \sqrt{u d (u)}$ $D e m o n s t r a t e t h a t \forall n \in N, I_{n + 1} - I_{n} = {(1 - u)}^{n} u^{\frac{3}{2}} d (u) a n d d e d u c e t h e m e a n i n g o f v a r i a t i o n s o f (I_{n}) \in N$

Question Number 171021 Answers: 0 Comments: 0

Question Number 171039 Answers: 1 Comments: 0

I_n =∫_0 ^1 (1−u)^n (√(ud(u))) Demonstrate that ∀n∈N, I_n ≥0

$I_{n} = \int_{0}^{1} {(1 - u)}^{n} \sqrt{u d (u)}$ $D e m o n s t r a t e t h a t \forall n \in N, I_{n} \geq 0$

Question Number 170953 Answers: 0 Comments: 3

Question Number 170855 Answers: 1 Comments: 0

⌊x⌋= log_2 (4^( x) −2^( x) −1)⇒ ⌊ 4^( x) ⌋=?

$⌊ x ⌋ = {l o g}_{2} (4^{x} - 2^{x} - 1) \Rightarrow ⌊ 4^{x} ⌋ = ?$

Question Number 170871 Answers: 1 Comments: 0

Why is it equal? (1/2)∫_0 ^π sin^(2p) udu=∫_0 ^(π/2) sin^(2p) udu

$W h y i s i t e q u a l ?$ $\frac{1}{2} \underset{0}{\int^{π}} {s i n}^{2 p} u d u = \underset{0}{\int^{\frac{π}{2}}} {s i n}^{2 p} u d u$

Question Number 170831 Answers: 2 Comments: 0

Question Number 170802 Answers: 2 Comments: 0

Question Number 170726 Answers: 0 Comments: 0

Question Number 170725 Answers: 1 Comments: 0

Question Number 170722 Answers: 2 Comments: 0

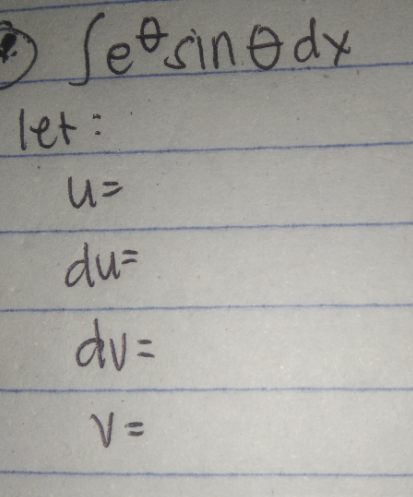
Question Number 170663 Answers: 2 Comments: 1

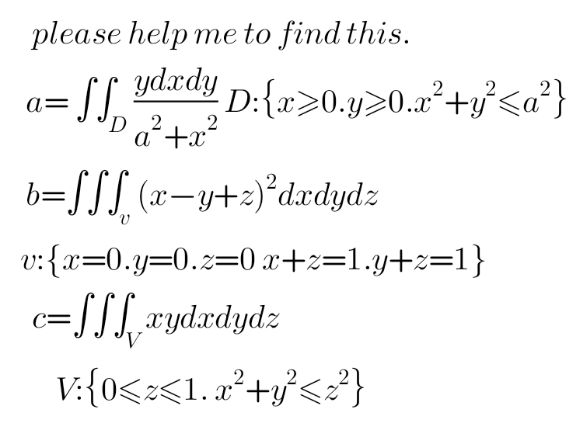
Question Number 170610 Answers: 1 Comments: 0

Pg 35 Pg 36 Pg 37 Pg 38 Pg 39 Pg 40 Pg 41 Pg 42 Pg 43 Pg 44

Contact: info@tinkutara.com