Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 45

Question Number 165787 Answers: 2 Comments: 0

find ∫cos^3 x dx ?

$f i n d \int {c o s}^{3} x d x ?$

Question Number 165757 Answers: 1 Comments: 0

Question Number 165742 Answers: 0 Comments: 0

prove that Σ_(n=0) ^∞ (((2n)!)/((n!)^2 4^n (2n+1)^4 ))=^? (π/(96))(12𝛇(3)+8ln^3 (2)+2π^2 ln(2)) −−−−−−−−by M.A

$p r o v e t h a t$ $\underset{n = 0}{\sum^{\infty}} \frac{(2 n)!}{{(n!)}^{2} 4^{n} {(2 n + 1)}^{4}} \overset{?}{=} \frac{π}{96} (12 ζ (3) + 8 \ln^{3} (2) + 2 π^{2} \ln (2))$ $- - - - - - - - b y M . A$

Question Number 165741 Answers: 2 Comments: 0

∫_0 ^π (dt/(1−sina.cost))=??? , a∈]0,(π/2)[

$\int_{0}^{π} \frac{d t}{1 - s i n a . c o s t} = ? ? ?, a \in] 0, \frac{π}{2} [$

Question Number 165685 Answers: 2 Comments: 0

_0 ∫^2 ∣ x^2 −2x+1 ∣ dx =?

$_{0} \int^{2} ∣ x^{2} - 2 x + 1 ∣ d x = ?$

Question Number 165615 Answers: 1 Comments: 0

∫_( 0) ^( 1) (dx/( (√x) ((x)^(1/3) +(x)^(1/4) )))=?

$\int_{0}^{1} \frac{d x}{\sqrt{x} (\sqrt[3]{x} + \sqrt[4]{x})} = ?$

Question Number 165574 Answers: 0 Comments: 0

Question Number 165568 Answers: 0 Comments: 0

Question Number 165550 Answers: 1 Comments: 0

Question Number 165426 Answers: 0 Comments: 1

prove that ζ (0 )= ((−1)/2)

$p r o v e t h a t$ $ζ (0) = \frac{- 1}{2}$

Question Number 165418 Answers: 0 Comments: 0

prove that : 1^∗ : Σ_(n=1) ^∞ (( ζ (2n )−1)/( 1+ n)) = (3/(2 )) − ln (π ) 2^( ∗∗) : Σ_(n=2) ^∞ (( (−1)^( n) ( ζ (n )−1 ))/(1 + n))=(3/2) +(γ/2) −((ln(8π))/2) 3^( ∗∗) : Σ_(n=1) ^∞ (( ζ (2n )−1)/(1+ 2n)) = (3/2) −((ln(4π))/2) −−−− m.n −−−−

$p r o v e t h a t :$ $1^{*} : \underset{n = 1}{\sum^{\infty}} \frac{ζ (2 n) - 1}{1 + n} = \frac{3}{2} - \ln (π)$ $2^{* *} : \underset{n = 2}{\sum^{\infty}} \frac{{(- 1)}^{n} (ζ (n) - 1)}{1 + n} = \frac{3}{2} + \frac{γ}{2} - \frac{\ln (8 π)}{2}$ $3^{* *} : \underset{n = 1}{\sum^{\infty}} \frac{ζ (2 n) - 1}{1 + 2 n} = \frac{3}{2} - \frac{\ln (4 π)}{2}$ $- - - - m . n - - - -$

Question Number 165380 Answers: 1 Comments: 0

∫_0 ^( (π/2)) (( x^( 3) )/(sin^( 2) (x)))dx=^? (3/8) (π^( 2) ln(4)−7ζ(3))

$\int_{0}^{\frac{π}{2}} \frac{x^{3}}{{s i n}^{2} (x)} d x \overset{?}{=} \frac{3}{8} (π^{2} l n (4) - 7 ζ (3))$

Question Number 165354 Answers: 0 Comments: 0

Question Number 165339 Answers: 1 Comments: 0

# Advanced Calculus # Let , f : R → Q is a continuous function . prove that ” f ” is a constant function . ■ m.n ∗ Adopted from mathematical analysis book ∗ −−−−−−−−−−−−−−

$You can't use 'macro parameter character #' in math mode$ $L e t, f : R \to Q i s a c o n t i n u o u s$ $f u n c t i o n . p r o v e t h a t^{″} f^{″} i s a$ $c o n s t a n t f u n c t i o n . ◼ m . n$ $* A d o p t e d f r o m m a t h e m a t i c a l a n a l y s i s b o o k *$ $- - - - - - - - - - - - - -$

Question Number 165329 Answers: 2 Comments: 0

prove ( n∈ N ) 3(n+1) ∣ n^( 3) + (n+1)^( 3) + (n+2 )^( 3)

$p r o v e (n \in N)$ $3 (n + 1) ∣ n^{3} + {(n + 1)}^{3} + {(n + 2)}^{3}$

Question Number 165320 Answers: 1 Comments: 0

Ω = ∫_0 ^( (π/4)) cos (2x ).e^( ⌊ sin(x)+ cos(x) ⌋) dx ⌊ x ⌋= max { m ∈ Z ∣ m ≤ x } −−−−

$Ω = \int_{0}^{\frac{π}{4}} c o s (2 x) . e^{⌊ s i n (x) + c o s (x) ⌋} d x$ $⌊ x ⌋ = m a x {m \in Z ∣ m ⩽ x}$ $- - - -$

Question Number 165255 Answers: 1 Comments: 0

nice integral ∫_0 ^1 (1/x)ln(Σ_(m=0) ^n x^m )dx=? −−−−−−−−−−−−−by MATH.AMIN

$nice integral$ $\int_{0}^{1} \frac{1}{x} \ln (\underset{m = 0}{\sum^{n}} x^{m}) dx = ?$ $- - - - - - - - - - - - - by MATH . AMIN$

Question Number 165218 Answers: 1 Comments: 1

Question by M.N July Φ = ∫_0 ^( 1) ((ln(1 + x^4 + x^8 ))/x)dx Φ =^(x=x^(1/2) ) (1/2)∫_0 ^( 1) ((ln(1+x^2 +x^4 ))/x)dx Φ = (1/2)∫_0 ^( 1) ((ln(((1−x^2 )/(1−x^6 ))))/x)dx = (1/2)∫_0 ^( 1) ((ln(1−x^2 ))/x)dx − (1/2)∫_0 ^( 1) ((ln(1−x^6 ))/x)dx Φ = (1/2)(A − B) A =^(x=x^(1/2) ) (1/2)∫_0 ^( 1) ((ln(1−x))/x)dx = (1/2)Li_2 (1) B =^(x=x^(1/6) ) (1/6)∫_0 ^( 1) ((x^((1/6)−1) ln(1−x))/x^(1/6) )dx B = (1/6)∫_0 ^( 1) ((ln(1−x))/x)dx = (1/6)Li_2 (1) Φ = (1/2)((1/2)Li_2 (1)−(1/6)Li_2 (1)) = (1/6)Li_2 (1) 𝚽 = ((𝛇(2))/3) ▲▲▲

Question Number 165183 Answers: 0 Comments: 1

Question Number 165164 Answers: 1 Comments: 0

Question Number 165271 Answers: 1 Comments: 0

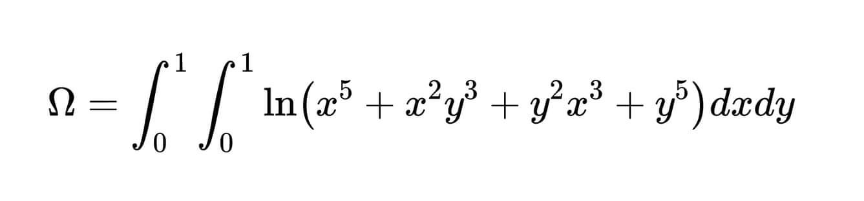
Let , f : [ 0 , 1 ] → R is a continuous function , prove that : lim_( n→ ∞) ∫_0 ^( 1) (( n f(x))/(1+ n^2 x^( 2) )) dx = (π/2) f (0 ) −−− proof −−− S_( n) = [∫_(0 ) ^( (1/( (√n)))) (( n. f(x))/(1 + n^( 2) x^( 2) )) dx =Ω_( n) ]+[ ∫_(1/( (√n))) ^( 1) ((n.f (x))/(1 + n^( 2) x^( 2) )) dx = Φ_( n) ] Ω_( n) =_(∃ t_( n) ∈ ( 0 , (1/( (√n) )) )) ^(MeanValueTheorem( first)) f (t_( n) )∫_(0 ) ^( (1/( (√n)))) (( n)/(1 + n^( 2) x^( 2) ))dx = f ( t_( n) ) ( tan^( −1) ( (√n) )) lim_( n→∞) (Ω_( n) ) = (π/2) f (lim_( n→∞) ( t_( n) ) ) = (π/2) f (0 ) Φ_( n) = ∫_(1/( (√n))) ^( 1) (( n. f(x) )/(1 + n^( 2) x^( 2) )) dx ⇒_(∃ M >0) ^(f is bounded) ∣ Φ_( n) ∣ ≤ M.∫_(1/( (√n))) ^( 1) (n/(1+ n^( 2) x^( 2) )) dx ⇒ ∣ Φ_( n) ∣ ≤ M . ( tan^( −1) ( n )− tan^( −1) ( (√n) )) lim_( n→ ∞) ∣ Φ_( n) ∣ = 0 ⇒ lim_( n→∞) Φ_( n) =0 ∴ lim_( n→ ∞) ( S_( n) ) = (π/2) f (0 ) ■ m.n

$L e t, f : [0, 1] \to R i s a c o n t i n u o u s$ $f u n c t i o n, p r o v e t h a t :$ ${l i m}_{n \to \infty} \int_{0}^{1} \frac{n f (x)}{1 + n^{2} x^{2}} d x = \frac{π}{2} f (0)$ $- - - p r o o f - - -$ $S_{n} = [\int_{0}^{\frac{1}{\sqrt{n}}} \frac{n . f (x)}{1 + n^{2} x^{2}} d x = Ω_{n}] + [\int_{\frac{1}{\sqrt{n}}}^{1} \frac{n . f (x)}{1 + n^{2} x^{2}} d x = Φ_{n}]$ $Ω_{n} \underset{\exists t_{n} \in (0, \frac{1}{\sqrt{n}})}{\overset{M e a n V a l u e T h e o r e m (f i r s t)}{=}} f (t_{n}) \int_{0}^{\frac{1}{\sqrt{n}}} \frac{n}{1 + n^{2} x^{2}} d x$ $= f (t_{n}) ({t a n}^{- 1} (\sqrt{n}))$ ${l i m}_{n \to \infty} (Ω_{n}) = \frac{π}{2} f ({l i m}_{n \to \infty} (t_{n})) = \frac{π}{2} f (0)$ $Φ_{n} = \int_{\frac{1}{\sqrt{n}}}^{1} \frac{n . f (x)}{1 + n^{2} x^{2}} d x \underset{\exists M > 0}{\overset{f i s b o u n d e d}{\Rightarrow}} ∣ Φ_{n} ∣ ⩽ M . \int_{\frac{1}{\sqrt{n}}}^{1} \frac{n}{1 + n^{2} x^{2}} d x$ $\Rightarrow ∣ Φ_{n} ∣ ⩽ M . ({t a n}^{- 1} (n) - {t a n}^{- 1} (\sqrt{n}))$ ${l i m}_{n \to \infty} ∣ Φ_{n} ∣ = 0 \Rightarrow {l i m}_{n \to \infty} Φ_{n} = 0$ $∴ {l i m}_{n \to \infty} (S_{n}) = \frac{π}{2} f (0) ◼ m . n$

Question Number 165273 Answers: 1 Comments: 0

lim_( n→ ∞) ∫_0 ^( 1) (( n . e^( 1− x^( 2) ) )/( 1 + n^( 2) x^( 2) )) dx =? −−−−−−

${l i m}_{n \to \infty} \int_{0}^{1} \frac{n . e^{1 - x^{2}}}{1 + n^{2} x^{2}} d x = ?$ $- - - - - -$

Question Number 165097 Answers: 1 Comments: 0

Question Number 165094 Answers: 0 Comments: 0

Question Number 165010 Answers: 0 Comments: 0

Ω= Σ_(n=1) ^∞ (( ψ^((2)) ( 1+ n ))/( n)) = ? −−− m.n −−−

$Ω = \underset{n = 1}{\sum^{\infty}} \frac{ψ^{(2)} (1 + n)}{n} = ?$ $- - - m . n - - -$

Question Number 164974 Answers: 1 Comments: 0

∫_0 ^( 1) (( ln( 1− x ).ln(x ) )/x^( (3/2)) )dx=^? π^( 2) −8ln(2 ) −−− m.n −−−

$\int_{0}^{1} \frac{\ln (1 - x) . \ln (x)}{x^{\frac{3}{2}}} d x \overset{?}{=} π^{2} - 8 \ln (2)$ $- - - m . n - - -$

Pg 40 Pg 41 Pg 42 Pg 43 Pg 44 Pg 45 Pg 46 Pg 47 Pg 48 Pg 49

Contact: info@tinkutara.com