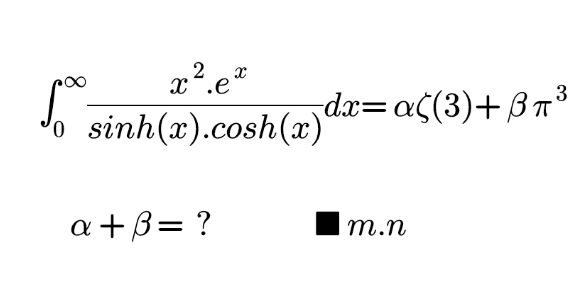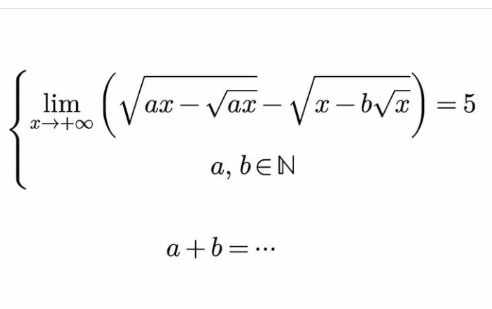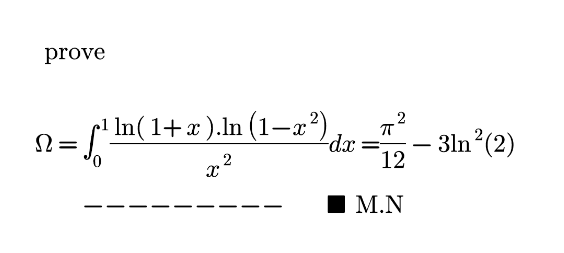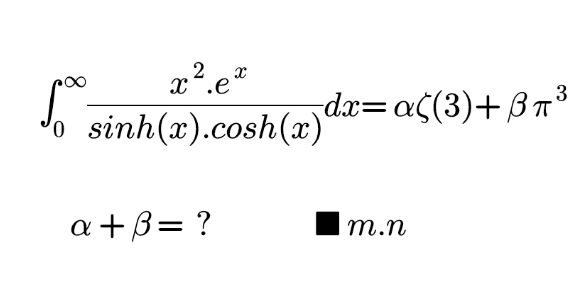|
|

|
All Questions Topic List |
IntegrationQuestion and Answers: Page 50 |
Question Number 164211 Answers: 1 Comments: 0
|

|
Question Number 164208 Answers: 0 Comments: 0
|

|
Question Number 164163 Answers: 2 Comments: 0
|
| Prove the;
∫_(−∞) ^∞ (1/(1 + x^2 )) dx = 𝛑
^({Z.A})
|
|
Question Number 164162 Answers: 0 Comments: 5
|
| Prove the;
(tan 𝛂 + ((cos 𝛂)/(1 + sin 𝛂))) sin 𝛂 = 𝛂
^([Z.A])
|
|
Question Number 164129 Answers: 1 Comments: 0
|
|
prove
𝛗= Re (∫_0 ^( 1) Li_( 2) ( (1/x) ) )dx = ζ (2)
−−−m.n−−−
|
|
Question Number 164123 Answers: 0 Comments: 0
|
| very nice to problem:
find in closed form;
∫_0 ^1 log (1−x^2 ) log^(n ) (1−x) dx;
n ∈ N^+
^(z.)
|
|
Question Number 164120 Answers: 0 Comments: 1
|
| How do you all to prove Integral;
Prove the;
∫ (((In x)2)/x) dx = (1/3) (In x)^3
|
|
Question Number 163954 Answers: 4 Comments: 0
|
|
Question Number 163854 Answers: 1 Comments: 0
|
| solution with residu theorem
∫_0 ^∞ (x^2 /(x^4 +2x^2 +2))dx=?
|
|
Question Number 163842 Answers: 1 Comments: 0
|
|
calculate
Ω = ∫_0 ^( 1) ((( Arctanh (x))/x^ ))^( 2) dx =?
−− m.n −−
|
|
Question Number 163838 Answers: 0 Comments: 0
|

|
Question Number 163829 Answers: 3 Comments: 1
|
| ∫(1/(cos x))
|
|
Question Number 163828 Answers: 2 Comments: 0
|
| ∫(e^x /x)
|
|
Question Number 163834 Answers: 0 Comments: 0
|
| ∫_0 ^∞ ((t(e^(4t) −1)(ln(i)+t))/e^(2t) )dt=?
by M.A
|
|
Question Number 163789 Answers: 0 Comments: 1
|
| ∫_0 ^1 ((arccotgh(x))/(1−x^2 ))dx=?
by M.A
|
|
Question Number 163785 Answers: 0 Comments: 0
|
| ∫_0 ^1 ((ln(x−1)ln(1−x))/x)dx=?
∫_0 ^1 ((ln(x−1)ln(1+x))/x)dx=?
by M.A
|
|
Question Number 163786 Answers: 1 Comments: 0
|
|
Question Number 163759 Answers: 3 Comments: 0
|
| ∫_0 ^1 (((ln(1+x))/x))^2 dx=?
by M.A
|
|
Question Number 163751 Answers: 1 Comments: 0
|
| ∫_0 ^1 ln(1+x)ln(1−x)dx=?
by MATH.AMIN
−−−−−−−−−−−−−−−−−−−−
|
|
Question Number 163709 Answers: 1 Comments: 0
|
| CALCULUS
∫_0 ^1 (x^(2n−1) /(x+1))dx=? n≥1
|
|
Question Number 163688 Answers: 2 Comments: 0
|
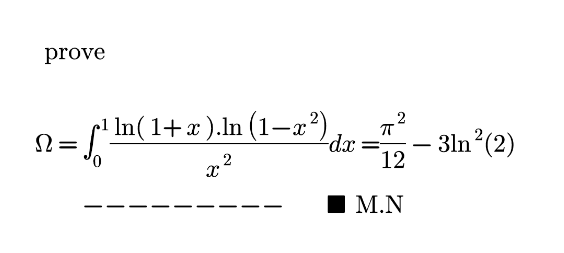
|
Question Number 163619 Answers: 1 Comments: 2
|
| Prove that;
∫_(−∞) ^0 e^(−∣t∣) dt = 1
|
|
Question Number 163614 Answers: 0 Comments: 0
|
| ∫((sec^2 x)/((secx+tanx)^(9/2) ))dx
|
|
Question Number 163577 Answers: 0 Comments: 0
|
| ∫_(−1) ^( 1) ((1/(1−ax)))ln (((1+x)/(1−x))) dx
|
|
Question Number 163574 Answers: 1 Comments: 0
|
| Show that;
∫_1 ^∞ ((In x)/x^4 ) dx = (1/9)
|
|
Question Number 163573 Answers: 0 Comments: 1
|

|
Pg 45
Pg 46
Pg 47
Pg 48
Pg 49
Pg 50
Pg 51
Pg 52
Pg 53
Pg 54
|
Terms of Service |
Privacy Policy |
Contact: info@tinkutara.com |