Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 51

Question Number 161609 Answers: 0 Comments: 0

∫_0 ^1 ((xln(1+x^4 ))/(1+x^2 ))dx=?

$\int_{0}^{1} \frac{x l n (1 + x^{4})}{1 + x^{2}} d x = ?$

Question Number 161537 Answers: 2 Comments: 0

∫_0 ^( (π/4)) ((1+tan^4 (x))/(cot^2 (x))) dx =?

$\int_{0}^{\frac{π}{4}} \frac{1 + \tan^{4} (x)}{\cot^{2} (x)} d x = ?$

Question Number 161443 Answers: 1 Comments: 0

Question Number 161412 Answers: 0 Comments: 0

Question Number 161407 Answers: 1 Comments: 0

Question Number 161404 Answers: 1 Comments: 0

Question Number 161393 Answers: 0 Comments: 0

Question Number 161329 Answers: 0 Comments: 0

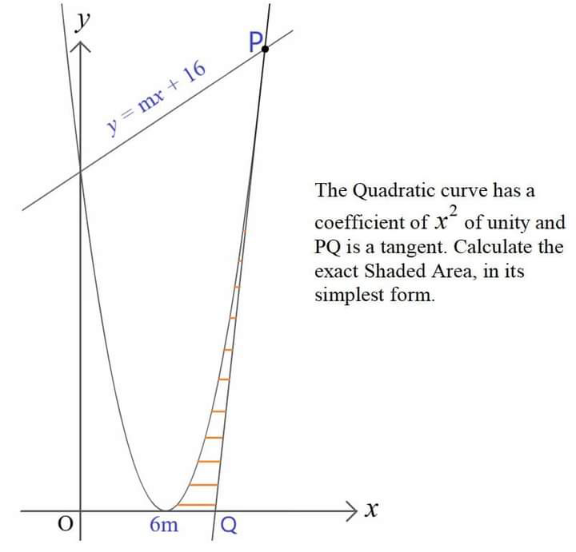
∫_1 ^( 2) ((tan^(−1) (x−1)log(x))/x)dx

$\int_{1}^{2} \frac{\tan^{- 1} (x - 1) \log (x)}{x} dx$

Question Number 161285 Answers: 5 Comments: 0

(1) ∫ (dx/(1−2cos x)) (2) ∫ ((sin 2x)/(sin x−sin^2 2x)) dx (3) ∫ (dx/(cos 2x−sin x))

$(1) \int \frac{d x}{1 - 2 \cos x}$ $(2) \int \frac{\sin 2 x}{\sin x - \sin^{2} 2 x} d x$ $(3) \int \frac{d x}{\cos 2 x - \sin x}$

Question Number 161281 Answers: 0 Comments: 0

Question Number 161265 Answers: 1 Comments: 2

Question Number 161256 Answers: 1 Comments: 0

Given f(x)=f(x+2), ∀x∈R If ∫_0 ^2 f(x)dx= p then ∫_0 ^(2020) f(x+2a)dx=? for a∈Z^+

$G i v e n f (x) = f (x + 2), \forall x \in R$ $I f \underset{0}{\int^{2}} f (x) d x = p t h e n \underset{0}{\int^{2020}} f (x + 2 a) d x = ?$ $f o r a \in Z^{+}$

Question Number 161233 Answers: 0 Comments: 0

Question Number 161229 Answers: 1 Comments: 0

Given f(x)= { ((1−∣x∣ ; x≤1)),((∣x∣−1 ; x>1)) :} find ∫_(−3) ^( 8) [f(x−1)+f(x+1)] dx.

$G i v e n f (x) = {\begin{cases} 1 - ∣ x ∣; x ⩽ 1 \\ ∣ x ∣ - 1; x > 1 \end{cases}$ $f i n d \int_{- 3}^{8} [f (x - 1) + f (x + 1)] d x .$

Question Number 161212 Answers: 2 Comments: 2

∫_( 0) ^( (π/2)) ((x sin x cos x)/(cos^4 x +sin^4 x)) dx =?

$\int_{0}^{\frac{π}{2}} \frac{x \sin x \cos x}{\cos^{4} x + \sin^{4} x} d x = ?$

Question Number 161178 Answers: 1 Comments: 0

∫^∞ _2 ((arctg(x))/(arctg((x/2))))dx=???

${\int_{2}}^{\infty} \frac{a r c t g (x)}{a r c t g (\frac{x}{2})} d x = ? ? ?$

Question Number 161176 Answers: 0 Comments: 0

calculate Θ := Σ_(n=1) ^∞ (( (−1 )^( n−1) )/(n ( n + (1/3) ))) =? ■ m.n −−−−−−−−−−−−−

$c a l c u l a t e$ $Θ := \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n - 1}}{n (n + \frac{1}{3})} = ? ◼ m . n$ $- - - - - - - - - - - - -$

Question Number 161100 Answers: 0 Comments: 0

f(x^2 )= 2+∫_( 0) ^( x^2 ) f(y) (1−tan y)dy , ∀x∈R f(−π)=?

$f (x^{2}) = 2 + \int_{0}^{x^{2}} f (y) (1 - \tan y) dy, \forall x \in R$ $f (- π) = ?$

Question Number 161089 Answers: 3 Comments: 0

prove that I= ∫_0 ^( (π/2)) ln ( 1+ sin (2 α )) dα = 2G − π ln ((√2) ) G: catalan constant

$p r o v e t h a t$ $I = \int_{0}^{\frac{π}{2}} \ln (1 + s i n (2 α)) d α$ $= 2 G - π \ln (\sqrt{2})$ $G : c a t a l a n c o n s t a n t$

Question Number 161076 Answers: 1 Comments: 0

Ω = ∫_0 ^( ∞) ((ln (1+ x ))/((1+ x^( 2) )^( 2) )) dx = ? −−−−−−−−−−−−

$Ω = \int_{0}^{\infty} \frac{l n (1 + x)}{{(1 + x^{2})}^{2}} d x = ?$ $- - - - - - - - - - - -$

Question Number 161003 Answers: 0 Comments: 0

Question Number 160982 Answers: 0 Comments: 0

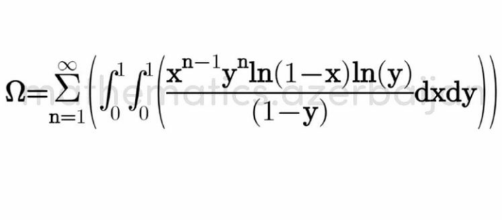
Ω = ∫_0 ^( 1) (( ln (−ln (x)))/(1+x)) dx =^? ((−1)/2) ln^( 2) (2)

$Ω = \int_{0}^{1} \frac{l n (- l n (x))}{1 + x} d x \overset{?}{=} \frac{- 1}{2} {l n}^{2} (2)$

Question Number 160979 Answers: 1 Comments: 0

Ω=∫_0 ^1 x^(n−1) ln(1−x)dx=??? n≥1

$Ω = \int_{0}^{1} x^{n - 1} \ln (1 - x) dx = ? ? ?$ $n ⩾ 1$

Question Number 160928 Answers: 1 Comments: 0

calculate Ω = Σ_(n=1) ^∞ (( ζ ( 1+ n ) −1)/(n + 1)) =^? 1− γ −−−−−−−−−−−

$c a l c u l a t e$ $Ω = \underset{n = 1}{\sum^{\infty}} \frac{ζ (1 + n) - 1}{n + 1} \overset{?}{=} 1 - γ$ $- - - - - - - - - - -$

Question Number 160902 Answers: 1 Comments: 0

∫ (dx/( (√(sin^3 x)) (√(cos^5 x)))) =?

$\int \frac{d x}{\sqrt{\sin^{3} x} \sqrt{\cos^{5} x}} = ?$

Question Number 160792 Answers: 2 Comments: 0

∫ ((sec x)/( (√(1+2sec x)))) (√((cosec x−cot x)/(cosec x+cot x))) dx =?

$\int \frac{\sec x}{\sqrt{1 + 2 \sec x}} \sqrt{\frac{cosec x - \cot x}{cosec x + \cot x}} dx = ?$

Pg 46 Pg 47 Pg 48 Pg 49 Pg 50 Pg 51 Pg 52 Pg 53 Pg 54 Pg 55

Contact: info@tinkutara.com