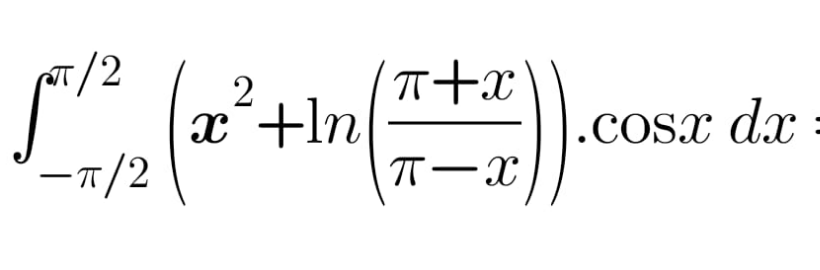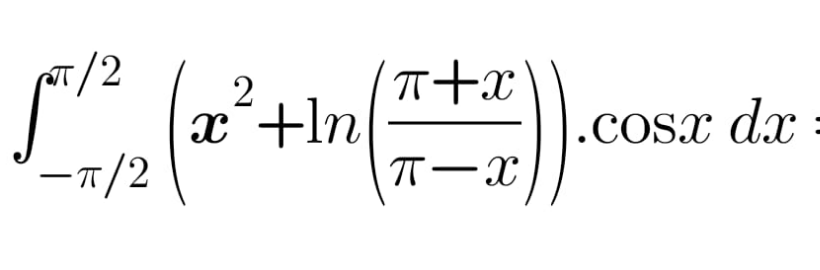Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 65

Question Number 152164 Answers: 1 Comments: 2

∫((2x+1)/(4−3x−x^2 ))dx

$\int \frac{2 x + 1}{4 - 3 x - x^{2}} dx$

Question Number 152163 Answers: 1 Comments: 0

∫(((x^2 +5x+3)/(x^2 +3x+2)))dx

$\int (\frac{x^{2} + 5 x + 3}{x^{2} + 3 x + 2}) dx$

Question Number 152161 Answers: 4 Comments: 0

∫cos (log x)dx

$\int \cos (\log x) dx$

Question Number 152160 Answers: 1 Comments: 0

∫[(1/(log x))−(1/((log x)^2 ))]dx

$\int [\frac{1}{\log x} - \frac{1}{{(\log x)}^{2}}] dx$

Question Number 152147 Answers: 1 Comments: 0

Question Number 152142 Answers: 1 Comments: 0

∫_0 ^1 (x/((1−x+x^2 )^2 ))ln(ln(1/x))dx=−(γ/3)−(1/3)ln((6(√3))/π)+((π(√3))/(27))(5ln2π−6lnΓ((1/6)))

$\int_{0}^{1} \frac{x}{{(1 - x + x^{2})}^{2}} \ln (\ln \frac{1}{x}) d x = - \frac{γ}{3} - \frac{1}{3} \ln \frac{6 \sqrt{3}}{π} + \frac{π \sqrt{3}}{27} (5 \ln 2 π - 6 \ln Γ (\frac{1}{6}))$

Question Number 152141 Answers: 2 Comments: 0

∫_0 ^(+∞) (((sinx)^(2n+1) )/x)dx=(π/2^(2n+1) ) (((2n)),(n) )

$\int_{0}^{+ \infty} \frac{{(\sin x)}^{2 n + 1}}{x} d x = \frac{π}{2^{2 n + 1}} (\begin{matrix} 2 n \\ n \end{matrix})$

Question Number 152140 Answers: 0 Comments: 0

I=∫_0 ^(2nπ) max(sinx, sin^(−1) (sinx))dx

$I = \int_{0}^{2 n π} \max (\sin x, \sin^{- 1} (\sin x)) d x$

Question Number 152115 Answers: 1 Comments: 0

∫(dx/(asin x+bcos x))

$\int \frac{dx}{asin x + bcos x}$

Question Number 152116 Answers: 3 Comments: 2

∫((sin x)/( (√(1+sin x))))dx

$\int \frac{\sin x}{\sqrt{1 + \sin x}} dx$

Question Number 152112 Answers: 1 Comments: 0

If I_n =∫((cos nx)/(cos x))dx then 1_n =?

$If I_{n} = \int \frac{\cos nx}{\cos x} dx then 1_{n} = ?$

Question Number 152111 Answers: 3 Comments: 0

∫tan^(−1) (sec x+tan x)dx

$\int \tan^{- 1} (\sec x + \tan x) dx$

Question Number 152110 Answers: 3 Comments: 0

∫a^(mx) b^(nx) dx

$\int a^{mx} b^{nx} dx$

Question Number 152106 Answers: 0 Comments: 0

∫ x^n cos(nx) dx

$\int x^{n} \cos (nx) dx$

Question Number 152094 Answers: 1 Comments: 0

Question Number 152088 Answers: 2 Comments: 0

∫_0 ^(Π/2) ∣sinx−cosx∣ please help me out

$\int_{0}^{\frac{Π}{2}} ∣ s i n x - c o s x ∣$ $p l e a s e h e l p m e o u t$

Question Number 152186 Answers: 1 Comments: 0

∫x^n cos(nx) dx

$\int x^{n} \cos (nx) dx$

Question Number 152047 Answers: 0 Comments: 0

∫_0 ^( ∞) ((x^2 +1)/( (√x^x ))) dx

$\int_{0}^{\infty} \frac{x^{2} + 1}{\sqrt{x^{x}}} d x$

Question Number 152105 Answers: 1 Comments: 0

∫_0 ^( ∞) (1/(⌊x+1⌋)) − (1/(x+1)) dx

$\int_{0}^{\infty} \frac{1}{⌊ x + 1 ⌋} - \frac{1}{x + 1} d x$

Question Number 151983 Answers: 1 Comments: 0

∫_(−∞) ^(+∞) (((1−ix)/(1+ix)))^n (((1+ix)/(1−ix)))^m (1/(1+x^2 ))dx

$\int_{- \infty}^{+ \infty} {(\frac{1 - i x}{1 + i x})}^{n} {(\frac{1 + i x}{1 - i x})}^{m} \frac{1}{1 + x^{2}} d x$

Question Number 151958 Answers: 0 Comments: 0

f ( x ) = a −(√((x/(1+x)) )) , D_( f) : [ 0, ∞) , a≥ 1 , h (x ):=(√(( f^( −1) (a−ax ))/(f^( −1) ( a− 2x )))) D_( h) = ? ( D := Domain )

$f (x) = a - \sqrt{\frac{x}{1 + x}}, D_{f} : [0, \infty)$ $, a ⩾ 1, h (x) := \sqrt{\frac{f^{- 1} (a - a x)}{f^{- 1} (a - 2 x)}}$ $D_{h} = ? (D := D o m a i n)$

Question Number 151951 Answers: 4 Comments: 1

nice ... mathematics S:= Σ_(n=1) ^∞ (( ζ (2n ))/(n . 16^( n) )) = ? ......■

$n i c e . . . m a t h e m a t i c s$ $S := \underset{n = 1}{\sum^{\infty}} \frac{ζ (2 n)}{n . 16^{n}} = ? . . . . . . ◼$

Question Number 151894 Answers: 1 Comments: 1

∫_0 ^a x (√((a^2 −x^2 )/(a^2 +x^2 )))

$\int_{0}^{a} x \sqrt{\frac{a^{2} - x^{2}}{a^{2} + x^{2}}}$

Question Number 151851 Answers: 1 Comments: 0

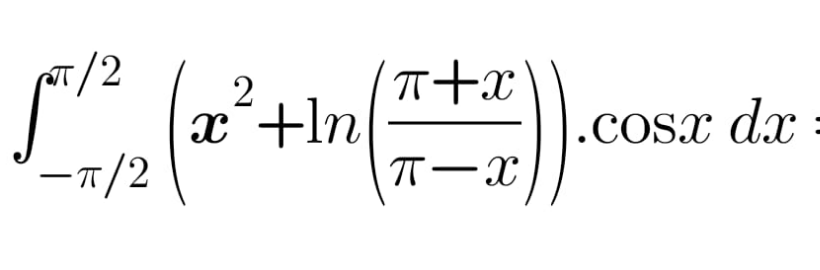
Question Number 151838 Answers: 0 Comments: 0

∫_0 ^( ∞) (((x^(log(⌊(⌊x⌋!)^((log(⌊x−1⌋!))^(−1) ) ⌋)+1) +1)^x )/(⌊x^(log(x^x )+1) ⌋!+1)) dx

$\int_{0}^{\infty} \frac{{(x^{\log (⌊ {(⌊ x ⌋!)}^{{(\log (⌊ x - 1 ⌋!))}^{- 1}} ⌋) + 1} + 1)}^{x}}{⌊ x^{\log (x^{x}) + 1} ⌋! + 1} d x$

Question Number 151860 Answers: 1 Comments: 3

∫_1 ^5 ∣2−∣3−x∣∣dx

$\underset{1}{\int^{5}} ∣ 2 - ∣ 3 - x ∣∣ dx$

Pg 60 Pg 61 Pg 62 Pg 63 Pg 64 Pg 65 Pg 66 Pg 67 Pg 68 Pg 69

Contact: info@tinkutara.com