
Question and Answers Forum
IntegrationQuestion and Answers: Page 67
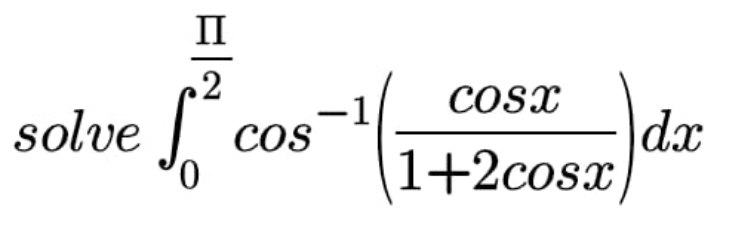


|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 67 |
| ∫_α ^β (dx/(x(√((x−α)(β−x) ))))=(π/( (√(αβ)))) where α,β >0 |
| Evaluate ∫_(−1) ^1 (((2x^(332) +x^(998) +4x^(1668) .sin x^(691) ))/(1+x^(666) ))dx |
| I = ∫_(x=a) ^( x=b) (√(u^2 + v^2 x^2 − 2uvwx)) dx = ? |
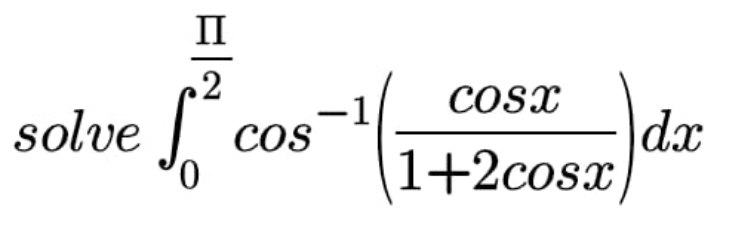
|
| Σ_(r=1) ^∞ (((−1)^(r−1) )/r)[ψ((r/2)+(1/4))−ψ((r/2)−(1/4))] |
| find I=∫_0 ^(π/4) ln(cosx)dx and J=∫_0 ^(π/4) ln(sinx)dx |
| prove: ∫_0 ^( ∞) (( ln ( 1+x^( 2) ))/(x^( 2) (1+x^( 2) )))dx= π ln((e/2) ) .. |
| ∫((sin x)/(sin (x−a)))dx |
| show that ∫_0 ^(π/2) ((cos x)/(cos x+sin x+1))dx=(1/4)(π−2ln 2) |
| ∫_0 ^( ∞) ((sin(2x)ln(x))/x) dx= m.∫_0 ^( ∞) (( ln(1+2x+x^2 ))/(x(ln^2 (x)+ π^( 2) ))) dx m=?.... |

|
| Calculate :: ∫_0 ^∞ ((sin (1145141919810893x))/(x(cosh x+cos x)))dx=(π/4) |
| Calculate :: ∫_0 ^∞ ((√x)/((x^4 +14x^2 +1)^(5/4) ))dx=((Γ^2 ((3/4)))/(4(√(2π)))) |
| Calculate :: ∫_0 ^π sin (x/2)∙arctan((2/(sin x))−1)dx=(√2)ln(1+(√2))+(1−(1/( (√2))))π |
| Calculate :: ∫_0 ^(π/2) (arctan(((sin x)/2))+arctan(((cos 3x+15cos x)/8)))dx =(π^2 /4)−ln^2 (1+(√2)) |
| Calculate :: ∫_(−∞) ^(+∞) ((Γ(x))/(Γ(x+a)))sin (πx)dx=(2^(a−1) /(Γ(a)))π (a>0) |
| Calculate :: ∫_0 ^π arctan(((2sin^2 x)/(1−2(√2)ϕcos x+2ϕ^2 )))dx=πarctan (√ϕ) (ϕ=(((√5)−1)/2)) |
| Calculate :: ∫_0 ^∞ ((ln(1+x))/((π^2 +ln^2 x)x))dx=γ |
| Calculate :: ∫_0 ^∞ (dx/( (√(x^2 +x))∙((8x^2 +8x+1))^(1/4) ))=((Γ^2 ((1/8)))/(2^((11)/4) Γ((1/4)))) |
| Calculate :: ∫_0 ^(π/2) x∙cot x∙ln^2 cos xdx=(π^3 /(24))ln2+(π/6)ln^3 2−(3/(16))πζ(3) |
| Calculate :: ∫_0 ^∞ ((x(√x))/((x^2 +1)(1+ax)))dx=((a^2 −a+(√(2a)))/( (√2)a(1+a^2 )))π ,(a>0) |
| Σ_(r=1,r≠s) ^n Σ_(s=1) ^n ((rs)/(n(n−1)))=^? (((n+1)(3n+2))/(12)) |
| Σ_(n=0) ^∞ (0^n /(n!))=? |

|
| ∫_0 ^( ∞) (ln(x^(√x) −1))^(−x) dx = ? |
| show that the improper integral lim_(B→∞) ∫_0 ^( B) sin(x)sin(x^2 )dx converges |