
Question and Answers Forum
IntegrationQuestion and Answers: Page 69
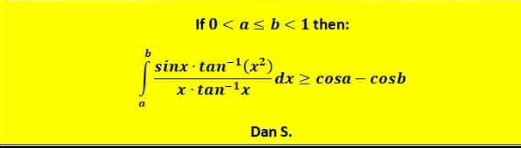

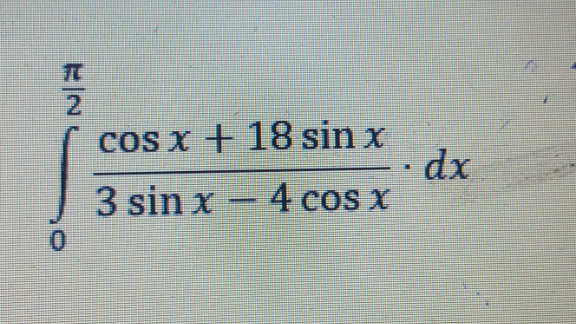
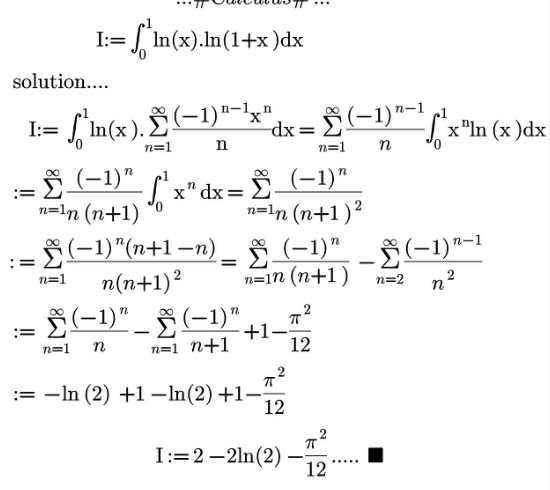

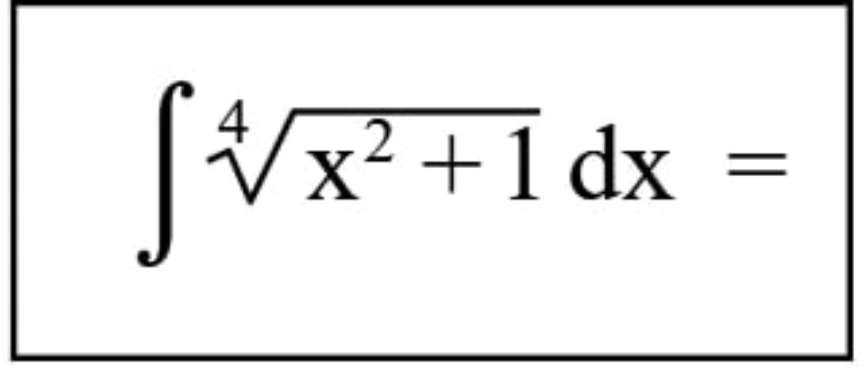
|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 69 |
| ∫_0 ^1 e^(−x) x^a dx a>0 |
| ∫(((√(2−x^2 ))+(√(2+x^2 )))/( (√(4−x^4 ))))dx |
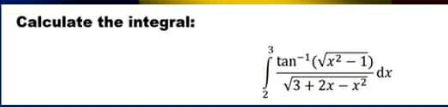
| ∫(((√(2−x^2 ))+(√(2+x^2 )))/( (√(4−x^2 ))))dx |
| ∫(((√(2−x^2 ))+(√(2+x^2 )))/( (√(4−x^4 ))))dx |

|
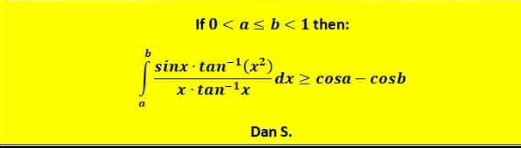
|
| let F(x)=(1/((x+1)^5 (2x−3)^4 )) 1) find ∫ F(x)dx 2)en deduire la decomposition de F en element simples |
| decompose F(x)=(1/((x^n −1)(x^2 +x+1))) dans C(x) puis dans R(x) |
| find by residus ∫_0 ^∞ ((cos(2x))/((x^2 −x+1)^3 ))dx |

|
| (1):: Σ_(i=1) ^n Σ_(j=1) ^n ∣i−j∣=? (2):: Σ_(i=1) ^n Σ_(j=i) ^n (1/j)=? (3):: Σ_(i=1) ^n^2 [(√i)]=? |
| (a , 2a +1 ]∩[ a^( 2) −a , a^( 2) + 4a +1 )≠ ∅ a ∈ ? |
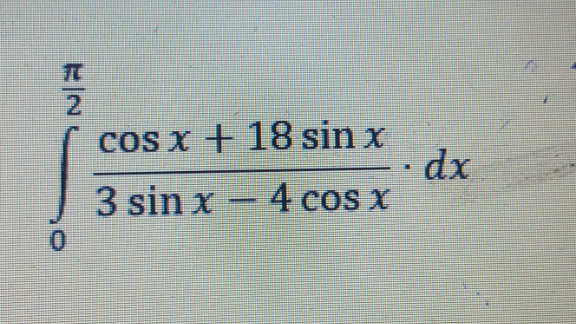
|
| ∫_0 ^(π/2) (e^(2arctg(u)) /( (√u))) |
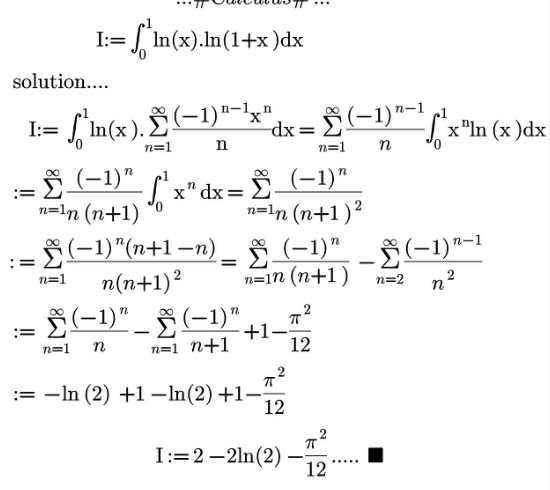
|

|
| ...Advanced Calculus... Calculate :: { (( i :: I := ∫_0 ^( 1) ln(x).ln(1+x) dx)),(( ii :: J := ∫_0 ^( 1) Li_( 2) ( 1− x^( 2) ) =?)) :} Note:: Li_2 (x) = Σ_(n=1) ^( ∞) (x^( n) /n^( 2) ) ........ ■ .... m.n.... |
| f(x)=∫_0 ^x e^(t−(t^2 /2)) dt show that ∫_0 ^1 f(t)dt=(√e)−1 |
| calculste ∫_0 ^1 (√(1+x^4 ))dx |
| find U_n =∫_0 ^∞ (e^(−nx^2 ) /(x^2 +n^2 ))dx (n≥1) nature of ΣU_n and Σ nU_n |
| find ∫_0 ^1 ((√x)/( (√(x^2 +3))+(√(2x^2 +1))))dx |
| ∫_R e^(ixt) e^(−t^2 ) dt.. |
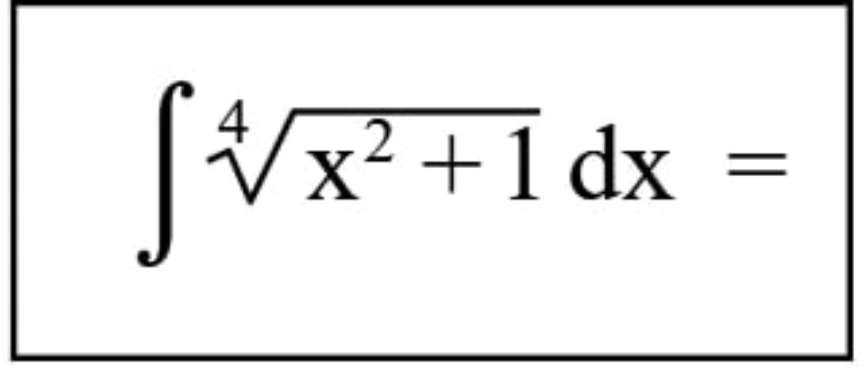
|
| find U_n =∫_0 ^1 (1+x^2 )(1+x^4 )....(1+x^2^n )dx |
| ∫_( 0 ) ^( ∞) (x^a /((1+x^3 ))) (dx/x) =? 0<a<3 |
| ∫_0 ^(π/2) e^(2x) (√(tanx))dx |