
Question and Answers Forum
IntegrationQuestion and Answers: Page 72


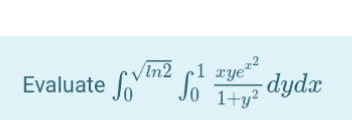




|
Question and Answers Forum |
IntegrationQuestion and Answers: Page 72 |
| Q :: # Calculus # If : 𝛗 ( n ) : = ∫_0 ^( 1) (( x^( 2n) )/(1 + x^( 2) )) dx then find the value of :: S := Σ_(n=1) ^∞ ((( −1 )^( n) 𝛗 ( n ))/n) = ? m.n.july.1970 |

|
| A region is enclosed by curves x^2 =4y, x^2 =−4y, x=4 & x=−4 V_1 is the volume of the solid obtained by rotating the above region round the y−axis. Another regions consists of points (x,y) satisfying x^2 +y^2 ≤16, x^2 +(y−2)^2 ≥4 and x^2 +(y+2)^2 ≥4 ,V_2 is the volume of the solid obtained by rotating this region round the y−axis Then V_1 =... |

|
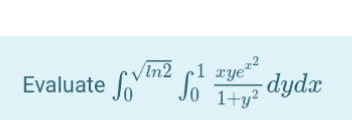
|

|
| On souhaite calculer I=∫_0 ^∞ ((sint)/t)dt. (1) On de^ finit la fonction F(x)=∫_0 ^∞ e^(−tx) ((sint)/t)dt. (a) De^ terminer le domaine de de^ finition de f sur R. (b) Montrer que F est de classe C^1 sur R_+ ^∗ et calculer F ′(x). (c) Limite de F en +∞ ? Conse^ quence ? (2) On note Si(t)=∫_0 ^t ((sinu)/u)du pour tout re^ el t. (a) Montrer que G(x)=∫_0 ^∞ e^(−tx) Si(t)dt est de^ finie sur R_+ ^∗ . (b) Montrer que xG(x)→I quand x→0^+ . (c) Au moyen d′une inte^ gration par parties, montrer que F est continue en 0. (3) Calculer I. |
| ......... Nice ......∗∗∗......Calculus......... f ( x ) : = [ tan (x) + cot (x) ] R_( f ) = ? Hint:: [ x ] := Max { m ∈Z ∣ m ≤ x } |
| .....calculus..... Ω := ∫_0 ^( ∞) ((sech(πx))/(1+4x^( 2) )) dx =^? (1/2) Ln(2) |
| ∫ (x^(n−1) /(x^(3n+1) (x^n −a))) dx ? |

|
| ........... Calculus........... In AB^Δ C : B^ = 2 C^ , a = λ b then specify the limits of the changes ′ λ ′ : |
| Triangle AOC inscribed in the region cut from the parabola y=x^2 by the line y=a^2 .Find the limit of ratio of the area of the triangle to the area of the parabolic region as a approaches zero |
| Find the areas of the regions enclosed by the lines and curves x=y^2 −1 and x=∣y∣(√(1−y^2 )) |
| let ϕ(x)=(1/(3+cosx)) developp f at fourier serie |
| ∫_0 ^( π/2) ((cos^2 x)/((2cos x+sin x)^2 )) dx =? |
| Find the volume of the region bounded by the elliptic paraboloid z = 4−x^2 −(1/4)y^2 and the plane z=0 |
| ..... Calculus (I )..... P:= ((∫_(0 ) ^( (π/2)) ( xcos(x)+1 )e^( sin(x)) dx )/(∫_0 ^( (π/2)) ( xsin(x) −1 )e^( cos(x )) dx))=? |
| .........Calculus(I)......... Lim_( x → 0) ((1 −cos(xcos((x/2)).cos((x/4))cos((x/8))))/x^( 2) )=? |
| ∫_0 ^∝ t^(n−2) costdt |
| ∫tan x sin^2 x cos^3 x cot^4 x dx =? |
| ...Advanced ....Calculus... Without using the Feynman′s trick , Find the value of :: I :=∫_0 ^( 1) ((Log (1+ x^( 2) ))/(1 +x)) dx=? m.n... |

|
| ∫ (dx/((x+3)(√(1−x^2 )))) ? |

|
| Σ_(i=1) ^n (((−1)^(n+1) )/n)=? |