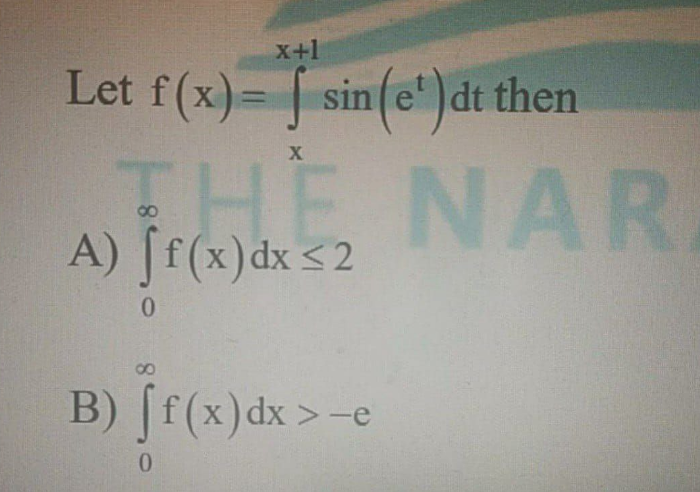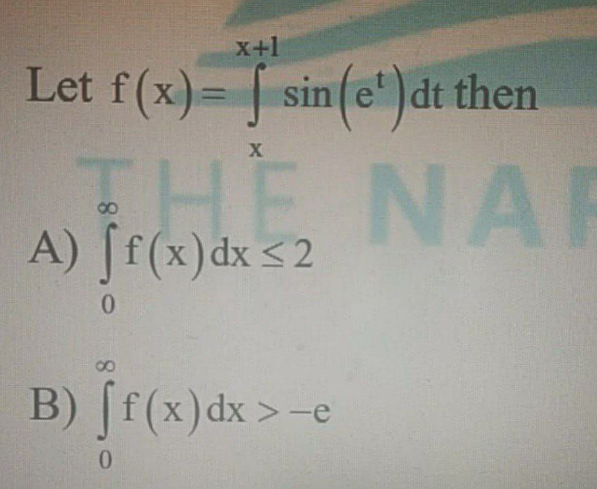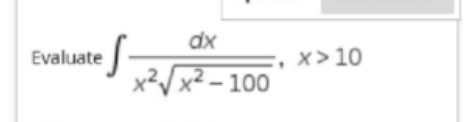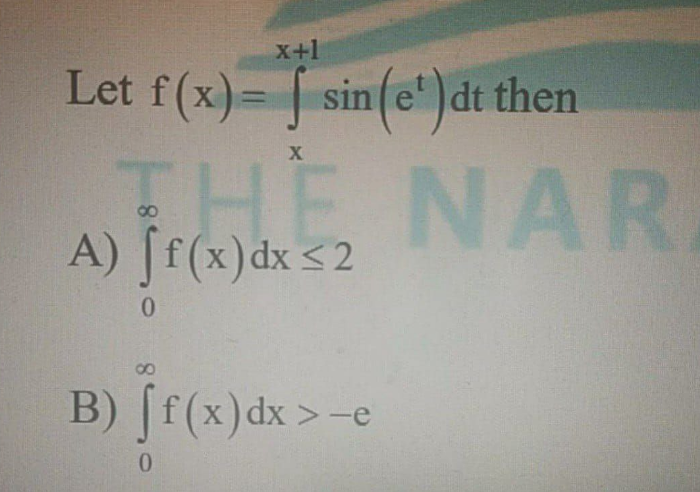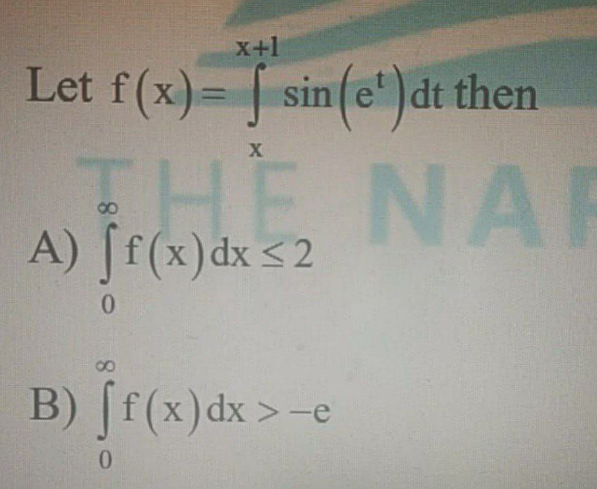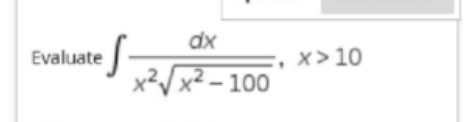Question and Answers Forum

All Questions Topic List

IntegrationQuestion and Answers: Page 73

Question Number 144432 Answers: 1 Comments: 0

∫_0 ^∝ t^(n−2) costdt

$\int_{0}^{\propto} t^{n - 2} c o s t d t$

Question Number 144431 Answers: 1 Comments: 0

∫tan x sin^2 x cos^3 x cot^4 x dx =?

$\int \tan x \sin^{2} x \cos^{3} x \cot^{4} x dx = ?$

Question Number 144419 Answers: 1 Comments: 0

...Advanced ....Calculus... Without using the Feynman′s trick , Find the value of :: I :=∫_0 ^( 1) ((Log (1+ x^( 2) ))/(1 +x)) dx=? m.n...

$. . . A d v a n c e d . . . . C a l c u l u s . . .$ $W i t h o u t u s i n g t h e {F e y n m a n}^{'} s t r i c k,$ $F i n d t h e v a l u e o f ::$ $I := \int_{0}^{1} \frac{L o g (1 + x^{2})}{1 + x} dx = ?$ $m . n . . .$

Question Number 144402 Answers: 1 Comments: 2

Question Number 144409 Answers: 2 Comments: 0

∫ (dx/((x+3)(√(1−x^2 )))) ?

$\int \frac{dx}{(x + 3) \sqrt{1 - x^{2}}} ?$

Question Number 144348 Answers: 1 Comments: 3

Question Number 144323 Answers: 1 Comments: 0

Σ_(i=1) ^n (((−1)^(n+1) )/n)=?

$\underset{i = 1}{\sum^{n}} \frac{{(- 1)}^{n + 1}}{n} = ?$

Question Number 144322 Answers: 1 Comments: 0

Σ_(n=0) ^∞ (((2n)!!)/((2n+1)!!(n+1)))x^(2n+2) =?..........∣x∣≤1

$\underset{n = 0}{\sum^{\infty}} \frac{(2 n)!!}{(2 n + 1)!! (n + 1)} x^{2 n + 2} = ? . . . . . . . . . . ∣ x ∣⩽ 1$

Question Number 144248 Answers: 1 Comments: 0

Question Number 144245 Answers: 2 Comments: 0

∫_0 ^1 (x^(2n) /((x−1)^n ))dx

$\int_{0}^{1} \frac{x^{2 n}}{{(x - 1)}^{n}} d x$

Question Number 144231 Answers: 1 Comments: 0

.....Nice ...Calculus if :: ϕ ( n ) := ∫_0 ^( 1) (x^( n) /(1 + x)) dx then :: Σ_(n=1) ^( ∞) (((−1)^(n−1) ϕ (n ))/n) =? ........

$. . . . . N i c e . . . C a l c u l u s$ $i f ::$ $φ (n) := \int_{0}^{1} \frac{x^{n}}{1 + x} d x$ $t h e n :: \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n - 1} φ (n)}{n} = ?$ $. . . . . . . .$

Question Number 144186 Answers: 2 Comments: 0

Estimate ∫_0 ^(0.5) (√(1+x^4 )) dx with an error 0.0001

$E s t i m a t e \int_{0}^{0.5} \sqrt{1 + x^{4}} d x$ $w i t h a n e r r o r 0.0001$

Question Number 144187 Answers: 1 Comments: 0

∫_0 ^(+∞) (u^2 /(u^8 +2u^4 +1))du

$\int_{0}^{+ \infty} \frac{u^{2}}{u^{8} + 2 u^{4} + 1} d u$

Question Number 144168 Answers: 1 Comments: 0

Question Number 144143 Answers: 1 Comments: 0

∫_(1/a) ^a ((arctg(x))/x)dx=???

$\int_{\frac{1}{a}}^{a} \frac{a r c t g (x)}{x} d x = ? ? ?$

Question Number 144142 Answers: 1 Comments: 0

∫ ((√(cos x+(√(cos x+(√(cos x+(√(cos x+(√(...))))))))))/(sin x)) dx

$\int \frac{\sqrt{\cos x + \sqrt{\cos x + \sqrt{\cos x + \sqrt{\cos x + \sqrt{. . .}}}}}}{\sin x} dx$

Question Number 144116 Answers: 0 Comments: 0

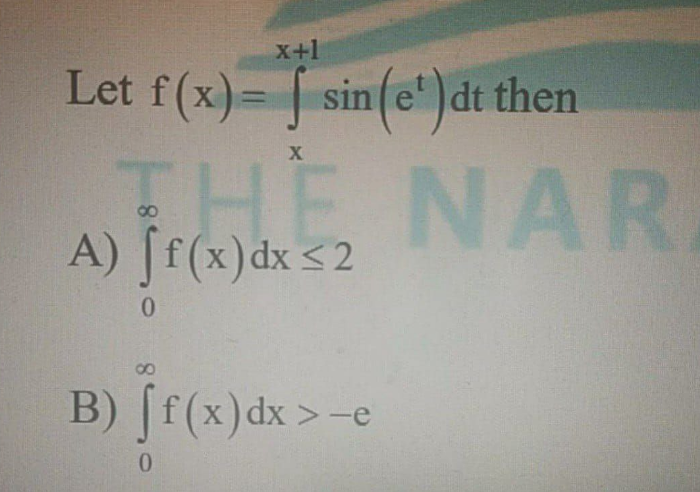
Question Number 144064 Answers: 2 Comments: 0

Question Number 144062 Answers: 0 Comments: 0

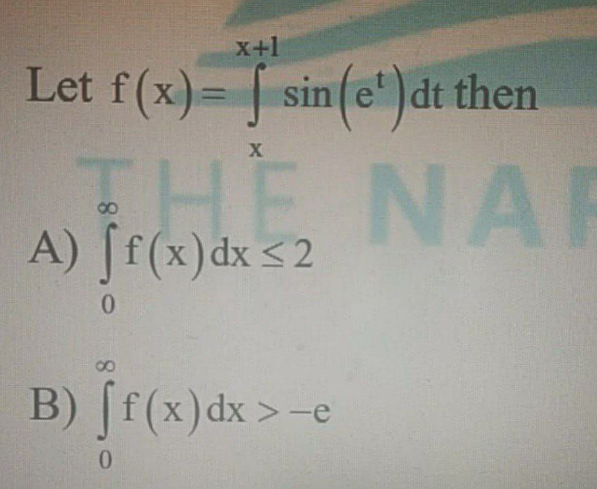
Question Number 144053 Answers: 1 Comments: 0

........ Calculus........ Ω:=lim(1/π)∫_0 ^( 2π) (Σ_(k=1) ^n ((sin(kx))/( (√2^k ))))^2 dx=?

$. . . . . . . . C a l c u l u s . . . . . . . .$ $Ω := l i m \frac{1}{π} \int_{0}^{2 π} {(\underset{k = 1}{\sum^{n}} \frac{s i n (k x)}{\sqrt{2^{k}}})}^{2} d x = ?$

Question Number 144052 Answers: 1 Comments: 0

Evaluate ∫ ((√x)/(sinh x)) dx

$Evaluate$ $\int \frac{\sqrt{x}}{\sinh x} d x$

Question Number 144042 Answers: 3 Comments: 0

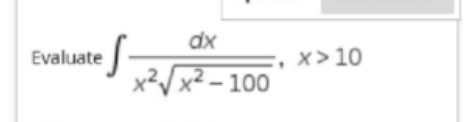
Question Number 144038 Answers: 0 Comments: 0

Question Number 144000 Answers: 1 Comments: 0

prove that ∀_m ∈N , a_k ,b_k ∈R cos^(2m) x =Σ_(k=1) ^m a_k cos 2kx cos^(2m−1) x=Σ_(k=1) ^m b_k cos (2k−1)x and find expr of a_k ,b_k in terms of k.

$prove that$ $\forall_{m} \in N, a_{k}, b_{k} \in R$ $\cos^{2 m} x = \underset{k = 1}{\sum^{m}} a_{k} \cos 2 k x$ $\cos^{2 m - 1} x = \underset{k = 1}{\sum^{m}} b_{k} \cos (2 k - 1) x$ $and find expr of a_{k}, b_{k} in terms of k .$

Question Number 143952 Answers: 3 Comments: 0

Question Number 143932 Answers: 4 Comments: 0

Pg 68 Pg 69 Pg 70 Pg 71 Pg 72 Pg 73 Pg 74 Pg 75 Pg 76 Pg 77

Contact: info@tinkutara.com