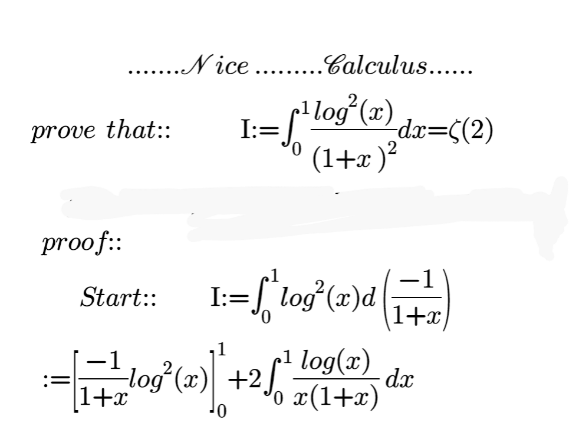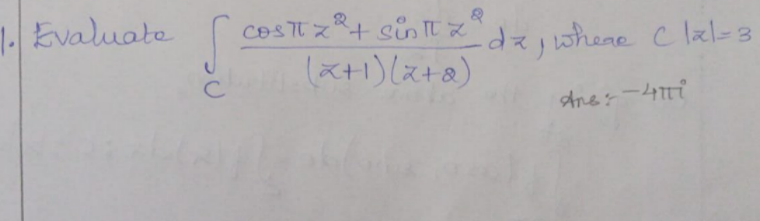|
|

|
All Questions Topic List |
IntegrationQuestion and Answers: Page 74 |
Question Number 143638 Answers: 0 Comments: 2
|
| ......Calculus....
𝛗:=^? ∫_0 ^( 1) ((ln(1−x)ln(x)(ln(((1−x)/x))))/x) dx
m.n....
|
|
Question Number 143628 Answers: 1 Comments: 0
|
| ∫_x ^∝ t^(α−1) e^(it) dt=??
|
|
Question Number 143622 Answers: 1 Comments: 0
|
| ∫_0 ^∝ e^(2arctg(t^2 )) dt
|
|
Question Number 143603 Answers: 2 Comments: 0
|
| .....Calculus.....
Ω:=Σ_(n=1) ^∞ (1/(n^k (1+n))) (k≥ 2) ......
|
|
Question Number 143588 Answers: 3 Comments: 0
|
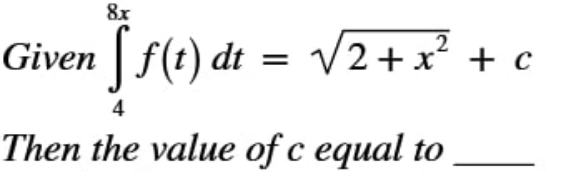
|
Question Number 143570 Answers: 1 Comments: 0
|

|
Question Number 143715 Answers: 0 Comments: 0
|
| ∫_0 ^(π/4) tanx∙Li(tan^2 x)dx
|
|
Question Number 143556 Answers: 0 Comments: 0
|
| ∫_0 ^∞ (dx/(x^α (lnx)^β ))
|
|
Question Number 143508 Answers: 3 Comments: 0
|
|
..........Calculus........
i: 𝛗_1 :=∫_0 ^( 1) ((ln^2 (1−x).ln(x))/x)dx
ii: 𝛗_2 := ∫_0 ^( 1) ((ln^2 (x).ln(1−x))/x) dx
iii : 𝛗_3 :=∫_0 ^( 1) ((ln^2 (x).ln(1+x))/x)dx
|
|
Question Number 143506 Answers: 1 Comments: 0
|
| ∫_1 ^∞ (1/(e^(−x) +e^x )) dx=?
|
|
Question Number 143502 Answers: 0 Comments: 0
|
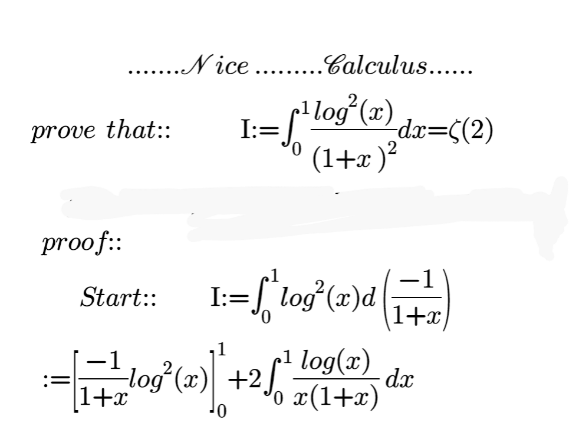
|
Question Number 143487 Answers: 0 Comments: 0
|
| find ∫_0 ^1 ((log(1+t^2 ))/(1+t))dt
|
|
Question Number 143477 Answers: 0 Comments: 0
|
| ∫_0 ^1 e^(2arctg(t^2 )) dt
|
|
Question Number 143474 Answers: 0 Comments: 0
|
| for all positive integral.,
u_(n+1) =u_n (u_(n−1) ^2 −2)−u_n
u_n =2 and u_1 =2(1/2)
prove that : 3log_2 [u_n ]=2^n −1(−1)^n
where [x] is the integral part of x
|
|
Question Number 143443 Answers: 1 Comments: 1
|

|
Question Number 143545 Answers: 2 Comments: 0
|
| calculate ∫_0 ^∞ ((logx)/(x^6 +1))dx
|
|
Question Number 143399 Answers: 2 Comments: 0
|
| ∫_0 ^(2π) (dx/((1−ksinx)^2 ))
|
|
Question Number 143312 Answers: 1 Comments: 0
|
| ∫_0 ^∞ ((sin^4 x)/x^4 )dx=(π/3)
|
|
Question Number 143248 Answers: 1 Comments: 1
|
| ∫(dx/(x^2 −4x+1))
|
|
Question Number 143230 Answers: 2 Comments: 0
|
| Σ_(n=1) ^∞ (x^(3n+1) /(3n+1))=?
|
|
Question Number 143219 Answers: 0 Comments: 1
|

|
Question Number 143210 Answers: 1 Comments: 0
|
| ∫_0 ^1 ((7^(x+1) +3^(x+1) )/(x+1))dx
|
|
Question Number 143192 Answers: 0 Comments: 0
|
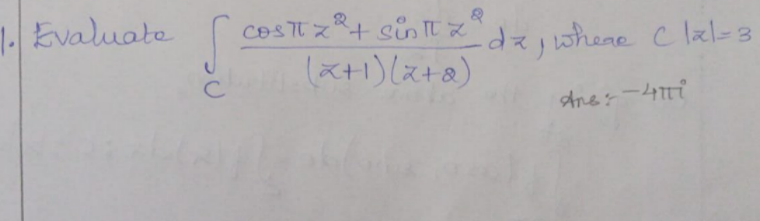
|
Question Number 143190 Answers: 1 Comments: 2
|
| ∫_R (e^(its) /(s+3))ds
|
|
Question Number 143178 Answers: 0 Comments: 2
|
| ∫_1 ^∞ ((x2^x +7)/(3^x +lnx+1))dx
|
|
Question Number 143163 Answers: 0 Comments: 0
|
| ∫_(1/x) ^x^2 (dt/( (√(1+t^3 )))) =?
|
|
Pg 69
Pg 70
Pg 71
Pg 72
Pg 73
Pg 74
Pg 75
Pg 76
Pg 77
Pg 78
|
Terms of Service |
Privacy Policy |
Contact: info@tinkutara.com |